COMP 555 – BioAlgorithms – Spring 2017

Lecture 2: Searching for patterns in data

From Daniel Becker's VisualDNA project

From Chapter 1 of "Bioinformatics Algorithms: An Active Learning Approach," Compeau & Pevzner

1

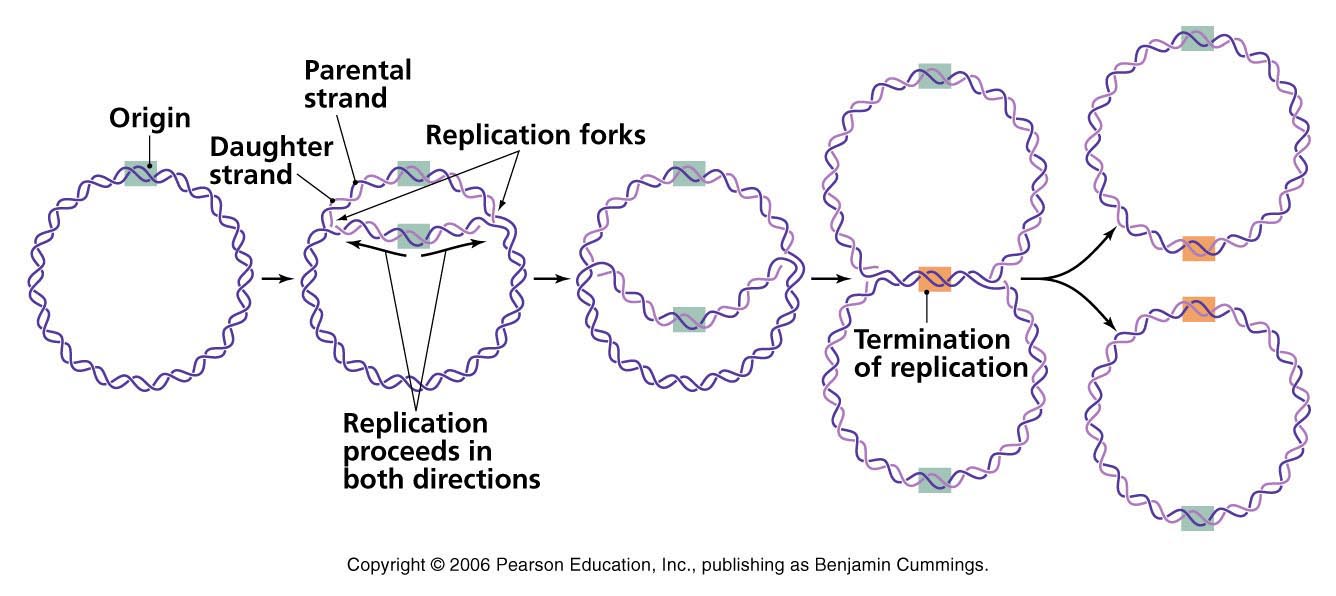
Life ≡ Reproduction ≡ Replicating a Genome

One of the most incredible things about DNA is that it provides instructions for replicating itself. Today, rather than looking for those instructions we consider how the process initiates.



2

Where Does Replication Begin?

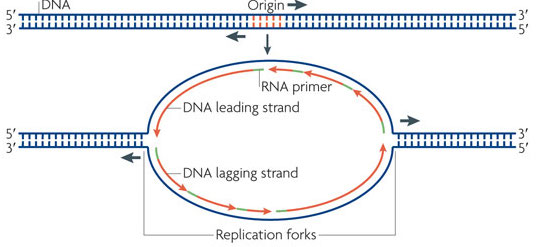
The DNA replication process begins reliably at a regions of the genome called the origins of replication or oriC. Today we investigate how these regions are identified?

3

Let's Start with Bacterial Genomes

In order to simplify our problem, we first consider Bacterial DNA.

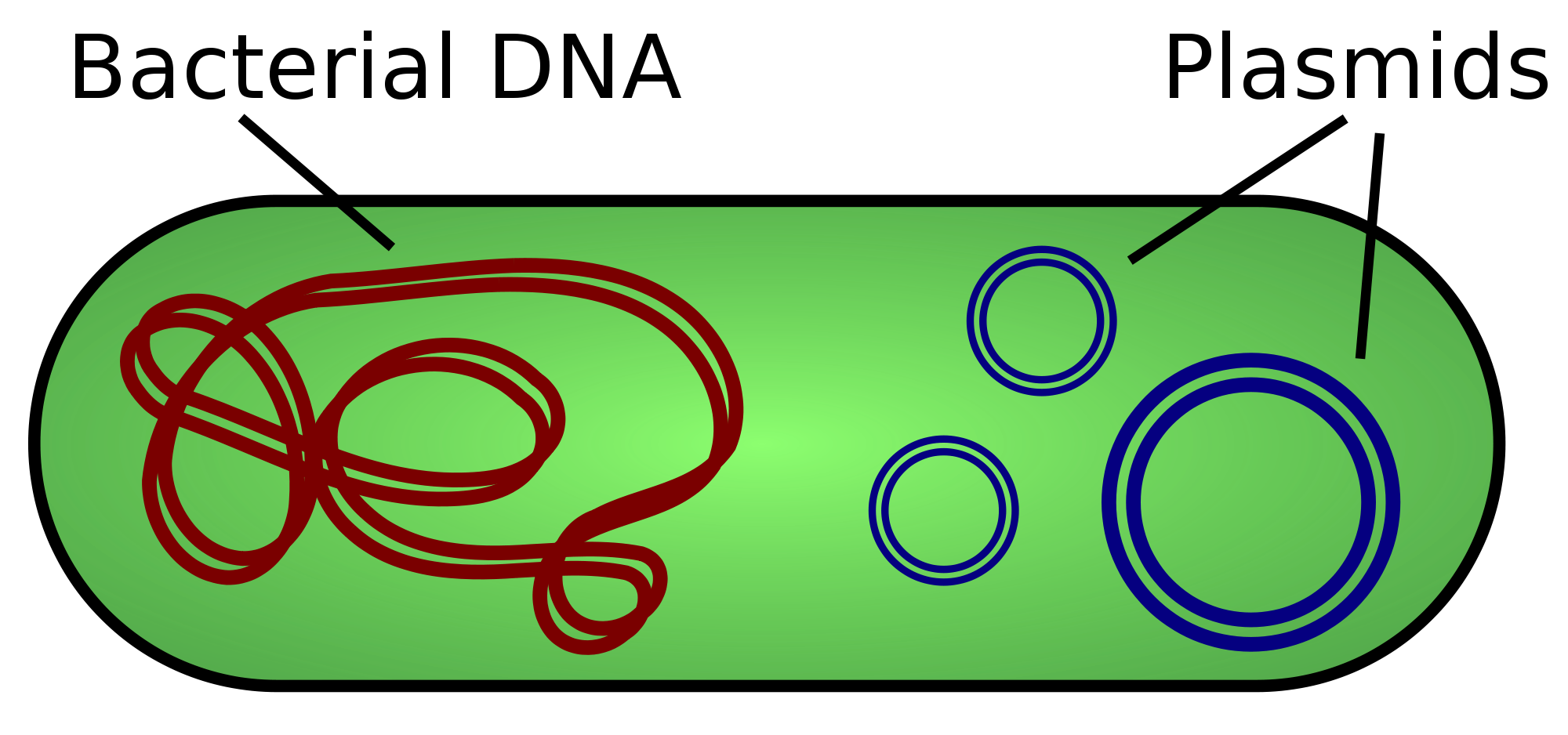
Characteristics of Bacterial DNA

  • A Circular primary chromosome
  • Independent, and generally smaller, circular plasmids
  • Simple highly conserved mechanism
  • Replication is constant (i.e. no cell cycle)

4

A cartoon of the DNA replication process






5

The oriC  finding Problem

Given a genome, find the *oriC* regions.

Biology Approach
Advantage: You can start immediately
Disadvantage: It can take a long time 		Computer Science Approach
Advantage: It can be fast, and general
Disadvantage: Problem is not adequately specified

6

Let's look at an example oriC

The replication origin of Vibrio Cholerae:

atcaatgatcaacgtaagcttctaagcatgatcaaggtgctcacacagtttatccacaacctgagtggatgacatcaagataggtcgttg
tatctccttcctctcgtactctcatgaccacggaaagatgatcaagagaggatgatttcttggccatatcgcaatgaatacttgtgactt
gtgcttccaattgacatcttcagcgccatattgcgctggccaaggtgacggagcgggattacgaaagcatgatcatggctgttgttctgt
ttatcttgttttgactgagacttgttaggatagacggtttttcatcactgactagccaaagccttactctgcctgacatcgaccgtaaat
tgataatgaatttacatgcttccgcgacgatttacctcttgatcatcgatccgattgaagatcttcaattgttaattctcttgcctcgac
tcatagccatgatgagctcttgatcatgtttccttaaccctctattttttacggaagaatgatcaagctgctgctcttgatcatcgtttc

Is there a pattern which might help us to develop an algorithm?

Vibrio Cholerae

Aquatic organism that causes Cholera

An abundant marine and freshwater bacterium that causes *Cholera*. Vibrio can affect shellfish, finfish, and other marine animals and a number of species are pathogenic for humans. ***Vibrio cholerae*** colonizes the mucosal surface of the small intestines of humans where it causes, a severe and sudden onset diarrheal disease.

One famous outbreak was traced to a contaminated well in London in 1854 by John Snow. Epidemics, which can occur with extreme rapidity, are often associated with conditions of poor sanitation. The disease is highly lethal if untreated. Millions have died over the centuries incuding seven major pandemics between 1817 and today. Six were attributed to the classical biotype, while the 7th, which started in 1961, is associated with this *El Tor* biotype.

7

An Aside: Accessing Sequence Data?

Genomes are archived as FASTA files, which are text files. Lines beginning with '>' are sequence headers. They are followed by lines of nucleotide sequences. Here's what one looks like:

In [2]:
!head data/VibrioCholerae.fa
!wc data/VibrioCholerae.fa
!grep ^\> data/VibrioCholerae.fa

>gi|146313784|gb|CP000626.1| Vibrio cholerae O395 chromosome 1, complete genome
ACAATGAGGTCACTATGTTCGAGCTCTTCAAACCGGCTGCGCATACGCAGCGGCTGCCATCCGATAAGGT
GGACAGCGTCTATTCACGCCTTCGTTGGCAACTTTTCATCGGTATTTTTGTTGGCTATGCAGGCTACTAT
TTGGTTCGTAAGAACTTTAGCTTGGCAATGCCTTACCTGATTGAACAAGGCTTTAGTCGTGGCGATCTGG
GTGTGGCTCTCGGTGCGGTTTCAATCGCGTATGGTCTGTCTAAATTTTTGATGGGGAACGTCTCTGACCG
TTCTAACCCGCGCTACTTTCTGAGTGCAGGTCTACTCCTTTCGGCACTAGTGATGTTCTGCTTCGGCTTT
ATGCCATGGGCAACGGGCAGCATTACTGCGATGTTTATTCTGCTGTTCTTAAACGGCTGGTTCCAAGGCA
TGGGTTGGCCTGCTTGTGGCCGTACTATGGTGCACTGGTGGTCACGCAAAGAGCGTGGTGAGATTGTTTC
GGTCTGGAACGTCGCTCACAACGTCGGTGGTGGTTTGATTGGCCCCATTTTCCTGCTCGGCCTATGGATG
TTTAACGATGATTGGCGCACGGCCTTCTATGTCCCCGCTTTCTTTGCGGTGCTGGTTGCCGTATTTACTT
  59038   59050 4191517 data/VibrioCholerae.fa
>gi|146313784|gb|CP000626.1| Vibrio cholerae O395 chromosome 1, complete genome
>gi|147673035|ref|NC_009457.1| Vibrio cholerae O395 chromosome 2, complete genome


8

A Python function to parse FASTA files

In [30]:
def loadFasta(filename):
    """ Parses a classically formatted and possibly 
        compressed FASTA file into a list of headers 
        and fragment sequences for each sequence contained"""
    if (filename.endswith(".gz")):
        fp = gzip.open(filename, 'rb')
    else:
        fp = open(filename, 'rb')
    # split at headers
    data = fp.read().split('>')
    fp.close()
    # ignore whatever appears before the 1st header
    data.pop(0)     
    headers = []
    sequences = []
    for sequence in data:
        lines = sequence.split('\n')
        headers.append(lines.pop(0))
        # add an extra "+" to make string "1-referenced"
        sequences.append('+' + ''.join(lines))
    return (headers, sequences)

9

Example Usage

In [31]:
header, seq = loadFasta("data/VibrioCholerae.fa")

for i in xrange(len(header)):
    print header[i]
    print len(seq[i])-1, "bases", seq[i][:30], "...", seq[i][-30:]
    print

genome = seq[0]
print "oriC:"
OriCStart = 151887
oriC = genome[OriCStart:OriCStart+540]
for i in xrange(9):
    print "    %s" % oriC[60*i:60*(i+1)].lower()

gi|146313784|gb|CP000626.1| Vibrio cholerae O395 chromosome 1, complete genome
1108250 bases +ACAATGAGGTCACTATGTTCGAGCTCTTC ... CCGATAGTAGAGGTTTATACCATCGCAAAA

gi|147673035|ref|NC_009457.1| Vibrio cholerae O395 chromosome 2, complete genome
3024069 bases +GTTCGCCAGAGCGGTTTTTGACTAGCTTG ... TTTCTGGGTTAAACAGATACTCGGGGCTGG

oriC:
    atcaatgatcaacgtaagcttctaagcatgatcaaggtgctcacacagtttatccacaac
    ctgagtggatgacatcaagataggtcgttgtatctccttcctctcgtactctcatgacca
    cggaaagatgatcaagagaggatgatttcttggccatatcgcaatgaatacttgtgactt
    gtgcttccaattgacatcttcagcgccatattgcgctggccaaggtgacggagcgggatt
    acgaaagcatgatcatggctgttgttctgtttatcttgttttgactgagacttgttagga
    tagacggtttttcatcactgactagccaaagccttactctgcctgacatcgaccgtaaat
    tgataatgaatttacatgcttccgcgacgatttacctcttgatcatcgatccgattgaag
    atcttcaattgttaattctcttgcctcgactcatagccatgatgagctcttgatcatgtt
    tccttaaccctctattttttacggaagaatgatcaagctgctgctcttgatcatcgtttc

  • Outputs the header, length, the 1st 30 characters, and last 30 characters of each sequence in the file

    • Note the addition of a "+" as first character
    • Why might their be multiple sequences in a file?

  • Then it outputs a subsequence on the first sequence

    10

Looking for Interesting Patterns

• So let's look at our example oriC region to see if we can find any interesting patterns
• Still not sure what "interesting"  means yet
• So let's consider every pattern of a given length, k

A new well-specified problem: Find the frequency of all subsequences of length k, k-mers


    atcaatgatcaacgtaagcttctaagcatgatcaaggtgctcacacagtttatccacaac
    atca     caacg     ttctaa     atcaagg     acacagtt
     tcaa     aacgt     tctaag     tcaaggt     cacagttt
      caat     acgta     ctaagc     caaggtg     acagttta
       aatg     cgtaa     taagca     aaggtgc     cagtttat
        atga     gtaag     aagcat     aggtgct     agtttatc
         tgat     taagc     agcatg     ggtgctc     gtttatcc
       4-mers    5-mers     6-mers      7-mers       8-mers

• Let's count the occurence of every k-mer in a sequence, given a value for k. </div>

11

Code for counting k-mers

In a string of length N, there are N-k+1, substrings of length k

In [33]:
def kmerFreq(k, sequence):
    """ returns the count of all k-mers in sequence as a dictionary"""
    kmerCount = {}
    for i in xrange(len(sequence)-k+1):
        kmer = sequence[i:i+k]
        kmerCount[kmer] = kmerCount.get(kmer,0)+1
    return kmerCount

print kmerFreq(3, "TAGACAT")
print kmerFreq(3, "mississippi")

{'ACA': 1, 'TAG': 1, 'GAC': 1, 'AGA': 1, 'CAT': 1}
{'sis': 1, 'sip': 1, 'iss': 2, 'ppi': 1, 'ipp': 1, 'ssi': 2, 'mis': 1}

12

An exhaustive scan for patterns

  • Is there some obvious pattern?
  • Let's consider a range of "K" values
In [34]:
def mostFreqKmer(start, end, sequence):
    for k in xrange(start,end):
        kmerCounts = kmerFreq(k,sequence).items()
        kmerCounts = sorted(kmerCounts,reverse=True,key=lambda tup: tup[1])
        mostFreq = kmerCounts[0:5] 
        print k, mostFreq

mostFreqKmer(1,10,oriC)

1 [('T', 174), ('A', 136), ('C', 122), ('G', 108)]
2 [('TT', 55), ('AT', 54), ('TC', 48), ('GA', 47), ('TG', 47)]
3 [('TGA', 25), ('ATC', 21), ('GAT', 21), ('CTT', 17), ('TCA', 17)]
4 [('ATGA', 12), ('ATCA', 11), ('TGAT', 11), ('GATC', 10), ('CTTG', 9)]
5 [('GATCA', 8), ('TGATC', 8), ('ATGAT', 7), ('TCTTG', 6), ('ATCAA', 6)]
6 [('TGATCA', 8), ('ATGATC', 5), ('ATCAAG', 4), ('CTCTTG', 4), ('GATCAT', 4)]
7 [('ATGATCA', 5), ('TGATCAA', 4), ('TGATCAT', 4), ('TCTTGAT', 3), ('TTGATCA', 3)]
8 [('ATGATCAA', 4), ('TCTTGATC', 3), ('CTCTTGAT', 3), ('TTGATCAT', 3), ('TGATCAAG', 3)]
9 [('CTTGATCAT', 3), ('TCTTGATCA', 3), ('CTCTTGATC', 3), ('ATGATCAAG', 3), ('TTGATCATC', 2)]

13

Examine the result

Are two 5-mers repeated 8 times interesting? Surprizing? How about four 9-mers repeated 3 times?

14

k-mer Likelihoods

Under the assumption that all k-mers are equally likely, we'd expect a given k-mer to occur:

$$p(k) = \frac{1}{4^k}$$

So we expect a specific 5-mer once per 1024 bases, so having 8 in 535 (540 - 5) bases is more than expected. We also expect a specific 9-mer once per 262,144 bases, so having 3 in 531 (540 - 9) is much more than expected.

Moreover, is their any relationship between the 9-mers ATGATCAAG and CTTGATCAT?

    atcaatgatcaacgtaagcttctaagcATGATCAAGgtgctcacacagtttatccacaac
    ctgagtggatgacatcaagataggtcgttgtatctccttcctctcgtactctcatgacca
    cggaaagATGATCAAGagaggatgatttcttggccatatcgcaatgaatacttgtgactt
    gtgcttccaattgacatcttcagcgccatattgcgctggccaaggtgacggagcgggatt
    acgaaagcatgatcatggctgttgttctgtttatcttgttttgactgagacttgttagga
    tagacggtttttcatcactgactagccaaagccttactctgcctgacatcgaccgtaaat
    tgataatgaatttacatgcttccgcgacgatttacctCTTGATCATcgatccgattgaag
    atcttcaattgttaattctcttgcctcgactcatagccatgatgagctCTTGATCATgtt
    tccttaaccctctattttttacggaagaATGATCAAGctgctgctCTTGATCATcgtttc
</div>

15

Any Biological Insights to Guide us?

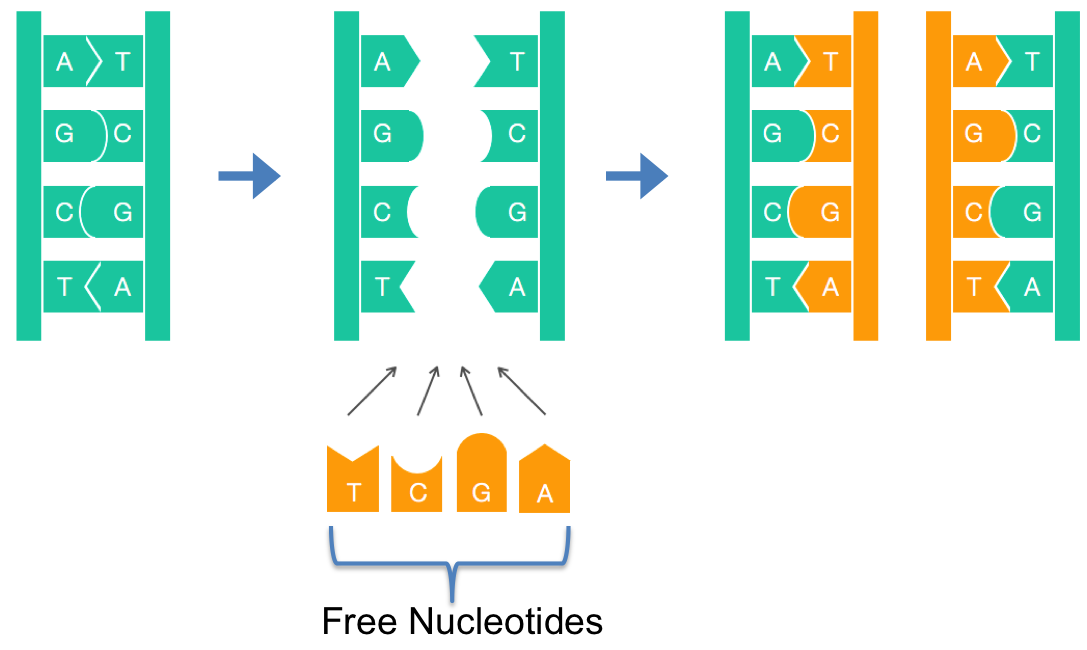
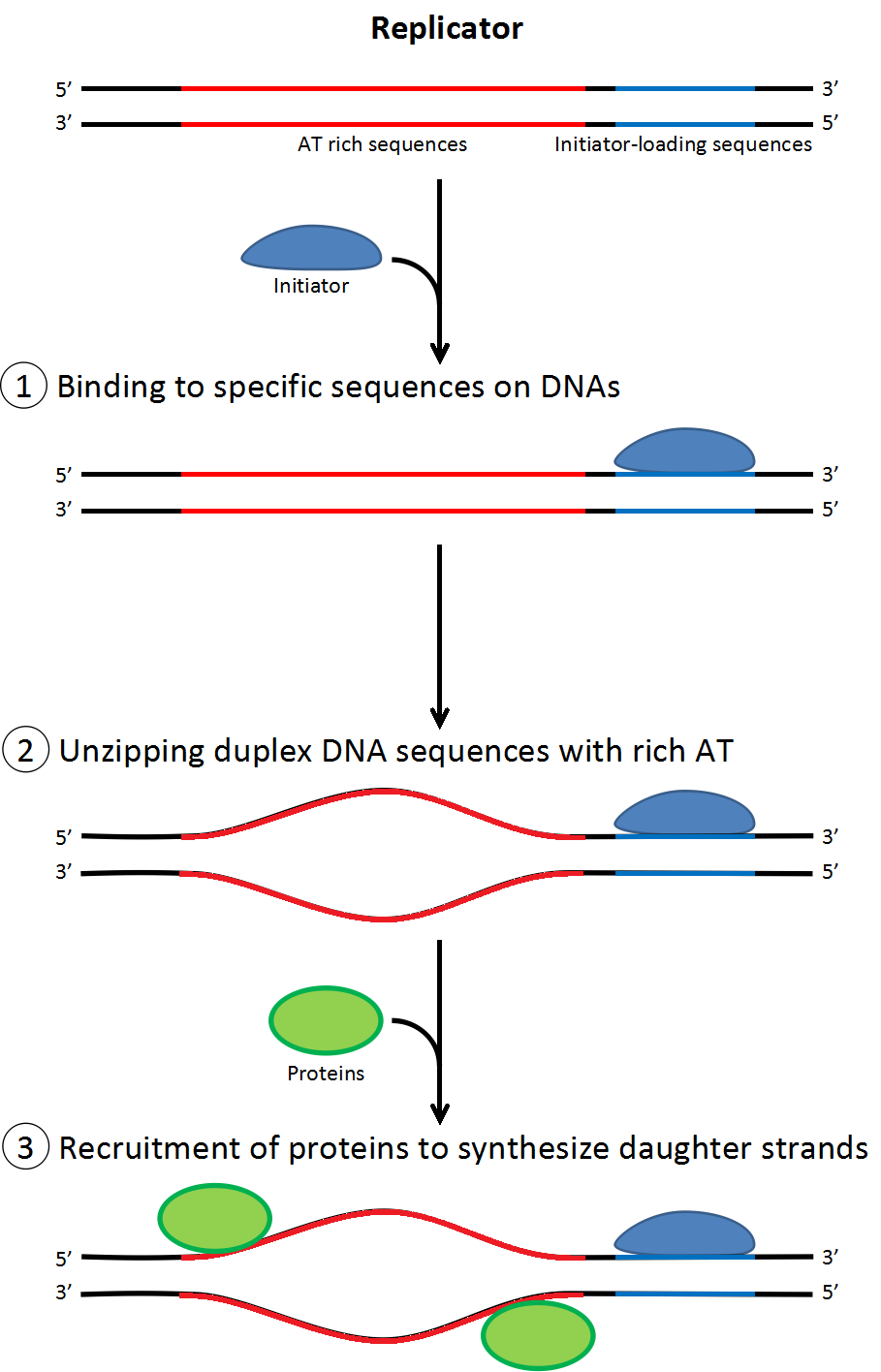
    • Replication is performed by a DNA polymerase, and the initiation of replication is mediated by a protein called DnaA.

    • DnaA binds to short (≈ 9 nucleotides long) segments within the replication origin known as a DnaA box (≈ 500 bases).

    • A DnaA box is a signal telling DnaA to “bind here!”

    • DnaA can bind to either strand. Thus, both the DnaA box and its reverse-complement are equal targets.

    • DnaA wants to see multiple DnaA boxes.

    • Sequences used by DnaA tend to be "AT-rich" (rich in adenine and thymine bases), because A-T base pairs have two hydrogen bonds (rather than the three formed in a C-G pair) which are easier to unzip. (Recall A-T was the second most common dimer with 54 after T-T with 55)

    • Once the origin has been located, these initiators recruit other proteins and form the pre-replication complex, which unzips the double-stranded DNA. </ul> </div>

    16

Do these Patterns Generalize?

Let's consider the OriC region of another bacteria Thermotoga petrophila

aactctatacctcctttttgtcgaatttgtgtgatttatagagaaaatcttattaactgaaactaaaatggtaggtttggtggtaggttt
tgtgtacattttgtagtatctgatttttaattacataccgtatattgtattaaattgacgaacaattgcatggaattgaatatatgcaaa
acaaacctaccaccaaactctgtattgaccattttaggacaacttcagggtggtaggtttctgaagctctcatcaatagactattttagt
ctttacaaacaatattaccgttcagattcaagattctacaacgctgttttaatgggcgttgcagaaaacttaccacctaaaatccagtat
ccaagccgatttcagagaaacctaccacttacctaccacttacctaccacccgggtggtaagttgcagacattattaaaaacctcatcag
aagcttgttcaaaaatttcaatactcgaaacctaccacctgcgtcccctattatttactactactaataatagcagtataattgatctga
aaagaggtggtaaaaaa

The most frequent 9-mers are: [(ACCTACCAC,5), (GGTAGGTTT,3), (CCTACCACC,3), (AACCTACCA,3), (TGGTAGGTT,3), (AAACCTACC,3)]

There is no occurence of the patterns ATGATCAAG and CTTGATCAT

Thus, it appears that different genomes have different DnaA box patterns. Let's go back to the drawing board. By the way, the DnaA box pattern of Thermotoga petrophila is:


                    CCTACCACC
                    |||||||||
                    GGATGGTGG
</div>

17

A New Strategy

  • Our previous strategy was to find frequent words in oriC region as candidate DnaA boxes, as if

replication origin → frequent words

  • Suppose that we reverse our approach, we use clumps of frequent words to infer the replication origin, testing if

nearby frequent words → replication origin

  • We can apply this approach to find candidate DnaA boxes.

18

What is a Clump?

We have an initition of what is meant by a clump of k-mers, but in order to define an algorithm we will need more precise definitons.

Formal Definition:
A k-mer forms an (L, t)-clump inside Genome if there is a short (length L) interval of Genome in which it appears many (at least t) times.

Clump Finding Problem:
Find patterns that form clumps within a string.
    **Input:** A string and integers *k* (length of a pattern), *L* (window length),
                 and *t* (number of patterns in a clump).
    **Output:** All k-mers forming (L,t) clumps in the string
</div>

19

K-mer counter that tracks positions

In [40]:
def kmerPositions(k, sequence):
    """ returns the position of all k-mers in sequence as a dictionary"""
    kmerPosition = {}
    for i in xrange(1,len(sequence)-k+1):
        kmer = sequence[i:i+k]
        kmerPosition[kmer] = kmerPosition.get(kmer,[])+[i]
    # combine kmers and their reverse complements
    pairPosition = {}
    for kmer in kmerPosition.iterkeys():
        krev = ''.join([{'A':'T','C':'G','G':'C','T':'A'}[base] for base in reversed(kmer)])   # one-liner
        if (kmer < krev):
            if (krev in kmerPosition):
                pairPosition[kmer] = kmerPosition[kmer] + kmerPosition[krev]
            else:
                pairPosition[kmer] = kmerPosition[kmer]
        elif (kmer == krev):
            pairPosition[kmer] = kmerPosition[kmer]
    return pairPosition


20

Lets play a little with that one-liner.

It is a Python list-comprehension. The Python language provides a rich set of tools not only for specifying algorithms, but also for specifying data structures. It can also specify *map-reduce* type operations on data structures, we'll discuss this in more detail later on.
In [41]:
mySeq = "GAGACAT"

print ''.join([{'A':'T','C':'G','G':'C','T':'A'}[base] for base in reversed(mySeq)])

ATGTCTC
The *join* method of a string combines the elements of the list it given using the given string as glue between them. Since our string is empty, '', it just glues them together. If we used a ',' string instead we'd get:
In [42]:
print ','.join([{'A':'T','C':'G','G':'C','T':'A'}[base] for base in reversed(mySeq)])
print ' and, '.join([{'A':'T','C':'G','G':'C','T':'A'}[base] for base in reversed(mySeq)])

A,T,G,T,C,T,C
A and, T and, G and, T and, C and, T and, C

21

More on List Comprehensions

The argument of the join method is a list construction shorthand called a list comprehension. It is basically a recipe for constructing a list. Here are some simple examples.

In [43]:
mySeq = "GAGACAT"

print [base for base in mySeq]
print [base for base in reversed(mySeq)]
print [base for base in reversed(mySeq) if base != 'A']

['G', 'A', 'G', 'A', 'C', 'A', 'T']
['T', 'A', 'C', 'A', 'G', 'A', 'G']
['T', 'C', 'G', 'G']

22

Back to Finding Clumps

By allowing each k-mer to appear in no more than 1 clump, we avoid smaller clumps reported within larger ones.
In [46]:
def findClumps(string, k, L, t):
    clumps = []
    kmers = kmerPositions(k, string)
    for kmer, posList in kmers.iteritems():
        i = 0
        while (i < len(posList)-t-1):
            foundSoFar = 1
            for j in xrange(i+1, len(posList)):
                if (((posList[j]+k) - posList[i]) > L):
                    break
                foundSoFar += 1
            if (foundSoFar >= t):
                clumps.append((kmer, foundSoFar))
            i = j
    return clumps

23

Now let's try it

In [48]:
clumpList = findClumps(genome, 9, 500, 6)
print len(clumpList)
print [clumpList[i] for i in xrange(min(20,len(clumpList)))]

24802
[('ACGCCATCC', 9), ('GGCACAGAA', 9), ('ACGCCATCA', 9), ('AGGCGGCAA', 15), ('GCCGCACAA', 16), ('CACAAAGCC', 14), ('AATTTGTGC', 9), ('ACCCAATGA', 7), ('ACCCAATGC', 8), ('ATGTTCACC', 7), ('AAATACGTC', 8), ('CGCGTTAGC', 10), ('CGCGCTGGC', 10), ('GGGCGATGA', 11), ('ATTCGTAAA', 9), ('ATTCGTAAC', 10), ('CGCTGCTGC', 15), ('ATTGCTCCA', 8), ('TATGCTGAA', 10), ('AACTATGGT', 8)]

Wow, that's a lot more than expected. I guess that means that genomes are not that random at all.

24

Let's view things differently

In [52]:
# Lets get the positions of all k-mers again
kmers = kmerPositions(9, genome)

top10 = ['ATGATCAAG'] + [kmer for kmer, clumpSize in sorted(clumpList,reverse=True,key=lambda tup: tup[1])[0:9]]
print top10

['ATGATCAAG', 'AACAAACGC', 'GCGTTTCCA', 'ACAAACGCC', 'AACGCCTCA', 'AGCCCCTTA', 'AGGCGGGCG', 'AAGAGGGAC', 'CAAGAGGGA', 'ACTGTCAAC']
In [54]:
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt

plt.figure(num=None, figsize=(12, 6), dpi=100, facecolor='w', edgecolor='k')
plt.plot([OriCStart, OriCStart], [0,10], 'k--')
for n, kmer in enumerate(top10):
    positions = kmers[kmer]
    plt.text(1120000, n+0.4, kmer, fontsize=8)
    plt.plot(positions, [n + 0.5 for i in xrange(len(positions))], 'o', markersize=4.0)
limit = plt.xlim((0,1250000))

25

Summary

Things have not gone as planned

  • We still don't have a working algorithm for finding OriC
  • We tried searching for patterns in a known OriC region, but the patterns we found did not generalize to other genomes.
  • We tried to find clumps of repeated k-mers, but that led to too many hypotheses to follow up on

But we won't give up

  • Let's see next time if there are any more biological insights that we might leverage

26

In [ ]: