SubBlock Recurrence¶
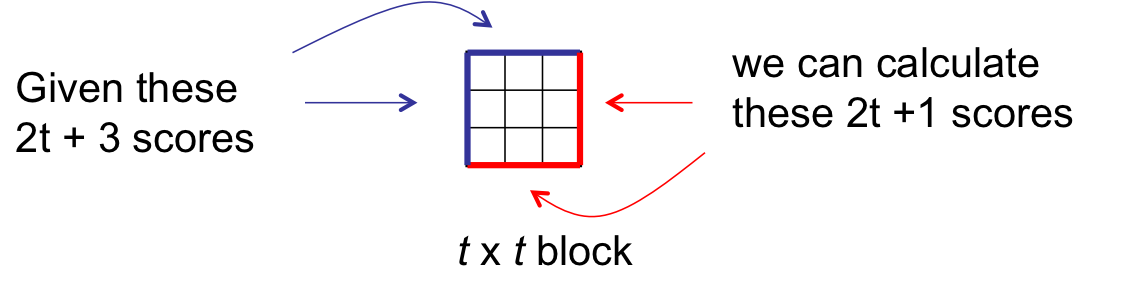
The Score lookup table is indexed by a pair of t-length sequences, so
$$o_1 = max \left( \begin{array}{cc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 2\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & -1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\infty\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\infty\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\infty\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\infty\\ \end{array} \right) % \left( \begin{array}{cc} i_1\\ i_2\\ i_3\\ i_4\\ i_5\\ i_6\\ i_7\\ i_8\\ i_9\\ 1 \end{array} \right) $$The right 2t+3 by 2t+3 elements are structrual
- differs per output $(o_1, o_2, ... o_7)$, but are shared by all sublocks
The left column depends on the two sequences
- inputs that do not impact the output have weights of $-\infty$
6
Speed up?¶
- Indices i,j range from 0 to n/t
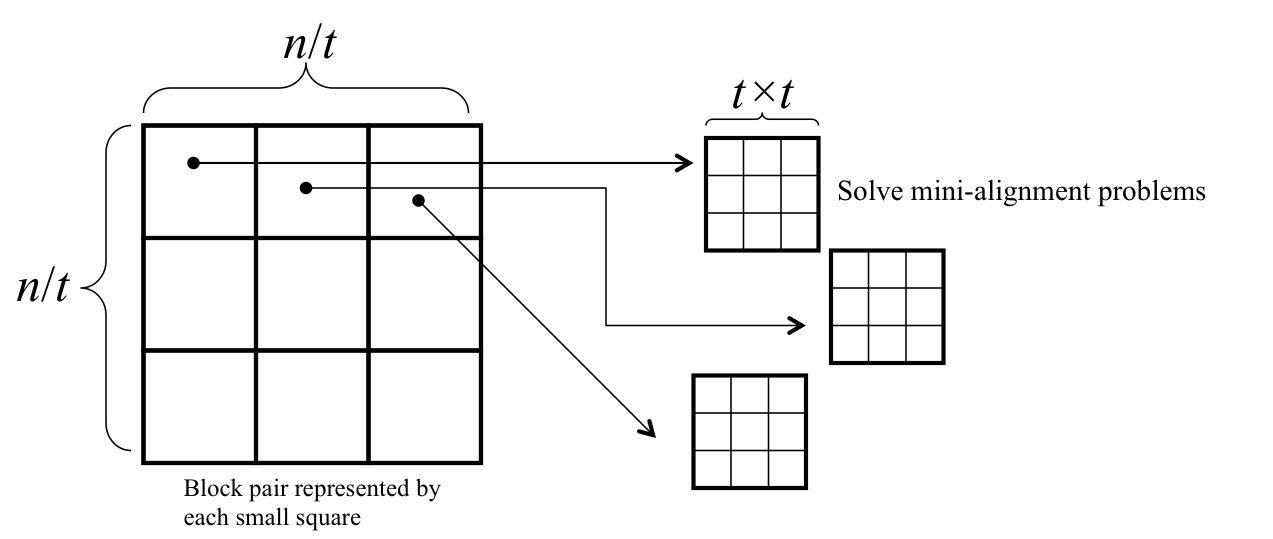
Running time of algorithm is $$O([n/t] [n/t] O(\beta_{i,j})) = O(n^2/t^2)$$
Computing all $\beta_{i,j}$ requires solving (n/t)(n/t) mini block alignments, each of size (tt)
So computing all $\beta_{i,j}$ takes time $$O((n^2/t^2) t^2) = O(n^2)$$
Looks like a wash, but is it?
7
Four Russians Technique¶
The trick is in how to pick t relative to n
If we pick $t = log_2(n)/4$
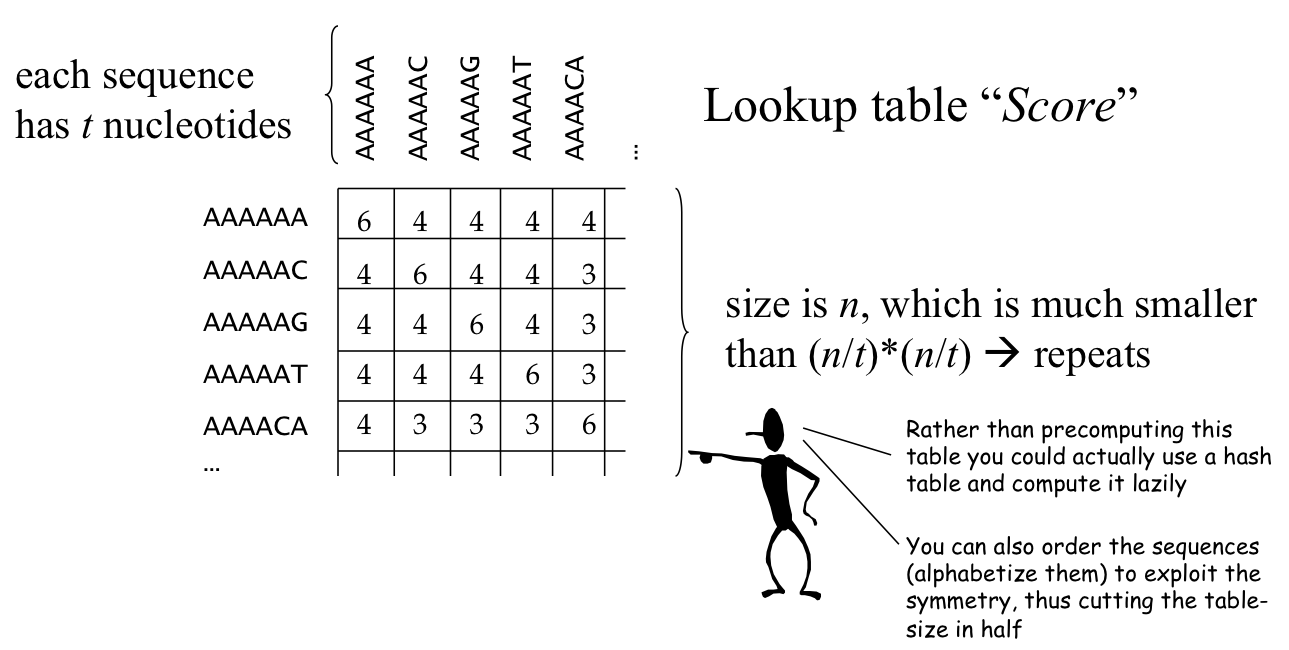
Instead of having (n/t) by (n/t) mini-alignments, construct 4t x 4t mini-alignments for all pairs of t nucleotide sequences, and put in a lookup table.
However, size of lookup table is not really that huge if t is small.
If $t = (log_2n)/4$. Then $4^t \times 4^t = \sqrt[4]{n^2} \times \sqrt[4]{n^2} = n$
Since computing the lookup table Score of size n takes $O(n)$ time, the running time is dominated by the (n/t) by (n/t) accesses to the lookup table
Overall running time: O( [n2/t2] )
Since t = (log2n)/4, substitute in: $$O \left( \frac{n^2}{{log_2n}^2} \right) = O \left( \frac{n^2}{log(n log n)} \right)$$
8