Divide and Conquer Algorithms

  • Midterm Status
  • Problem Set #3
  • Grading of Problem Sets #1 and #2

1

The Essence of Divide and Conquer

  • Divide problem into sub-problems
  • Conquer by solving sub-problems recursively.
    • If the sub-problems are small enough, solve them in brute force fashion
  • Combine the solutions of sub-problems into a solution of the original problem
    • This is the tricky part

2

Divide and Conquer Applied to Sorting

Problem

  • Given an unsorted array of items
52471326
  • Reorganize them such that they are in non-decreasing order
12234567

3

Mergesort: Divide Phase

Step 1 - Divide

52471326

           ↓              ↓

5247
1326

           ↓       ↓       ↓       ↓

52
47
13
26

          ↓   ↓   ↓   ↓   ↓   ↓   ↓   ↓

5
2
4
7
1
3
2
6

$log_2(n)$ divisions to split an array of size n into single elements

4

Mergesort: Combine Trick

Merge

  • 2 arrays of size 1 can be easily merged to form a sorted array of size 2
5
2
→
25
4
7
→
47
25
47
→
2457

  • Move the smaller first value of the two arrays to the next slot in the merged array. Repeat.

  • 2 sorted arrays of size p and q can be merged in $O(p+q)$ time to form a sorted array of size p+q

5

Mergesort: Conquer Step

Step 2 - Conquer

5
2
4
7
1
3
2
6

O(n)      ↓       ↓       ↓       ↓

25
47
13
26

O(n)     ↓              ↓

2457
1236

O(n)      ↓

12234567

$log_2(n)$ iterations, each iteration takes $O(n)$ time, for a total time $O(n log(n))$

6

Now back to Biology

All algorithms for aligning a pair of sequences thus far have required quadratic memory

The tables used by the dynamic programming method

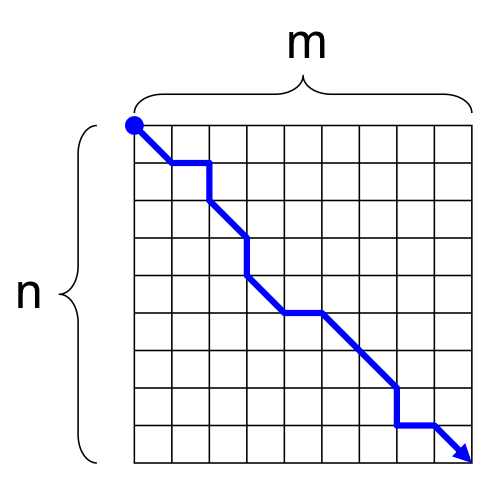
  • Space complexity for computing alignment path for sequences of length n and m is O(nm)
  • We kept a table of all scores and arrival directions in memory to reconstruct the final best path (backtracking)

7

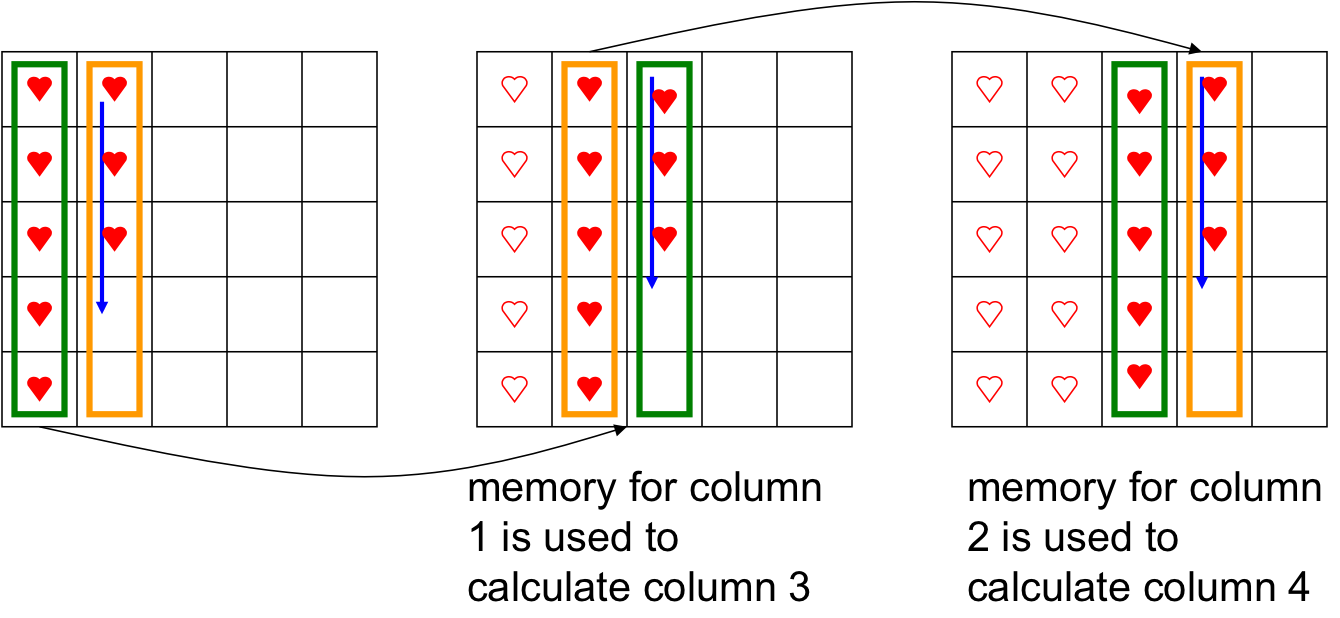
Computing Alignments with Linear Memory

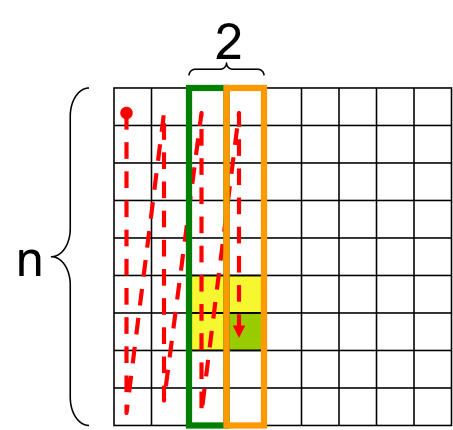
  • If appropriately ordered, the space needed to compute just the score can be reduced to O(n)
  • For example, we only need the previous column to calculate the current column, and we can throw away that previous column once we’re done using it

8

Recycling Columns

Only two columns of scores are needed at any given time

9

An Aside

Suppose that we reverse the source and destination of our Manhattan Tour

  • Does the path with the most attractions change?

10

More Aside

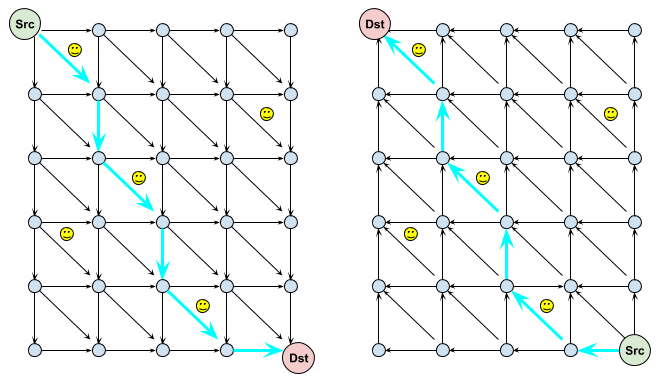
Now suppose that we made two tours

  • One from the source towards the destination
  • A second from the destination of towards the source
  • And we stop both tours at the middle column

  • Can we combine these two separate solutions to find the overall best score?

11

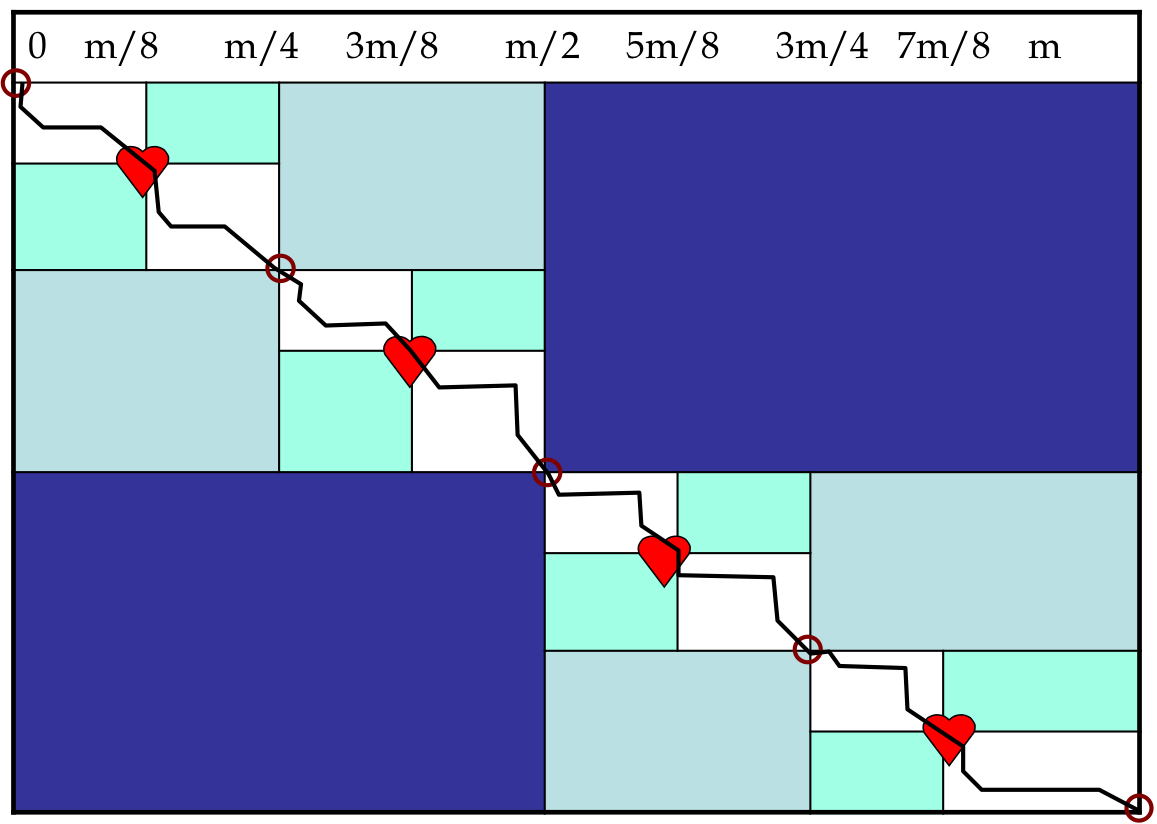
A D&C Approach to find the best Alignment score

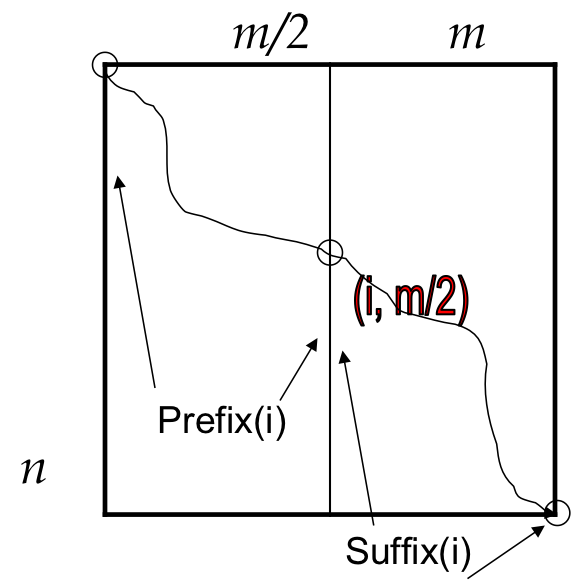
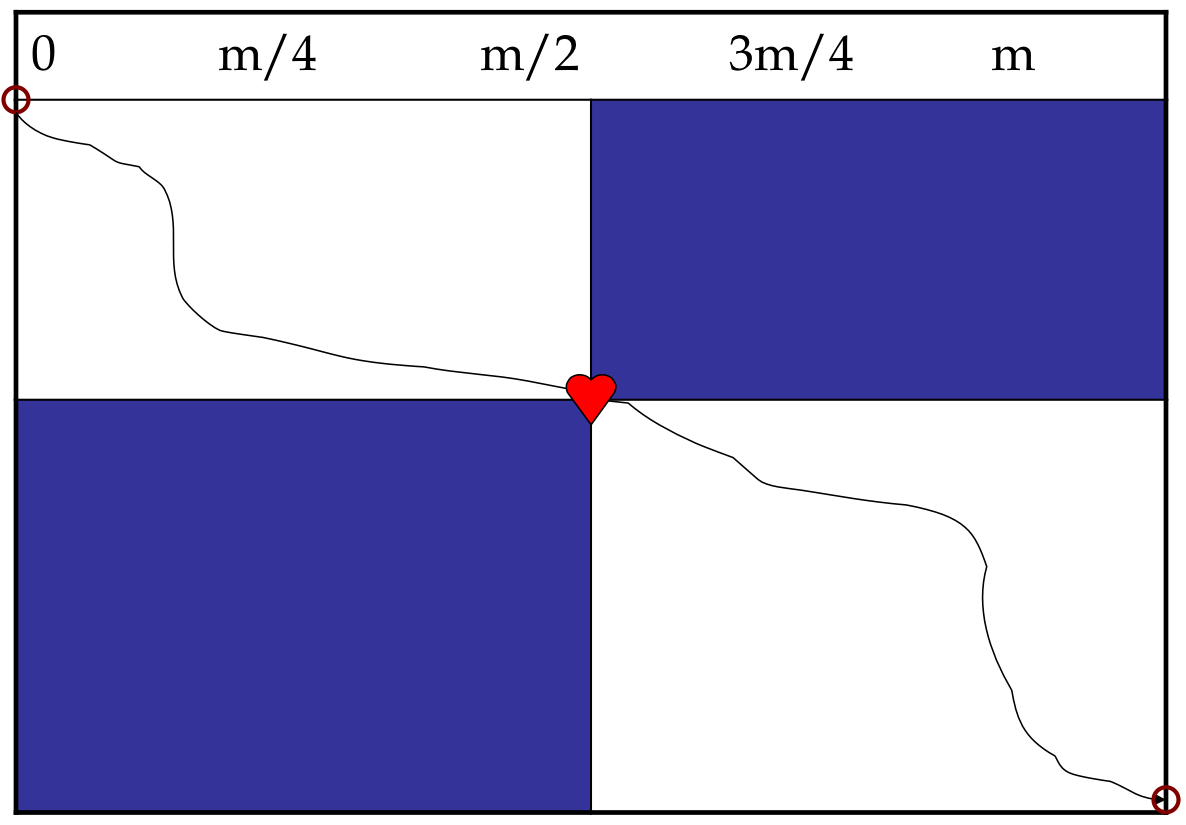
  • We want to calculate the longest path from (0,0) to (n,m) that passes through (i,m/2) where i ranges from 0 to n and represents the i-th row

  • Define Score(i) as the score of the path from (0,0) to (n,m) that passes through vertex (i, m/2)

12

Finding the Midline

Define (mid,m/2) as the vertex where the best score crosses the middle column.

  • How hard is the problem compared to the original DP approach?
  • What does it lack?

13

We know the Best Score

How do we find the best path?

  • We actually know one vertex on our path, (m/2, mid).
  • How do we find more?

  • Hint: Knowing mid actually constrains where the paths can go

14

A Mid's Mid

We can now solve for the paths from (0,0) to (m/2, mid) and (m/2, mid) to (m,n)

15

And Mid-Mid's Mids (recursively)

And repeat this process until the path is from (i,j) to (i,j)

16

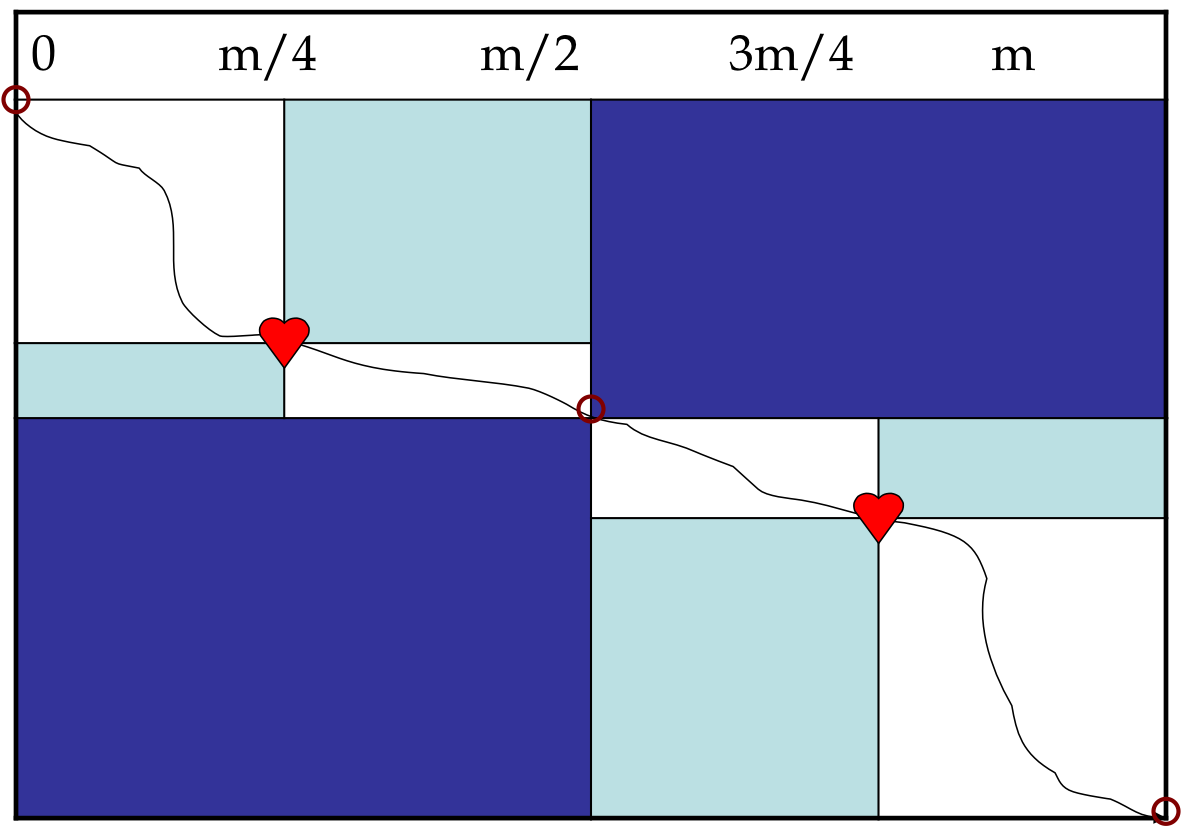
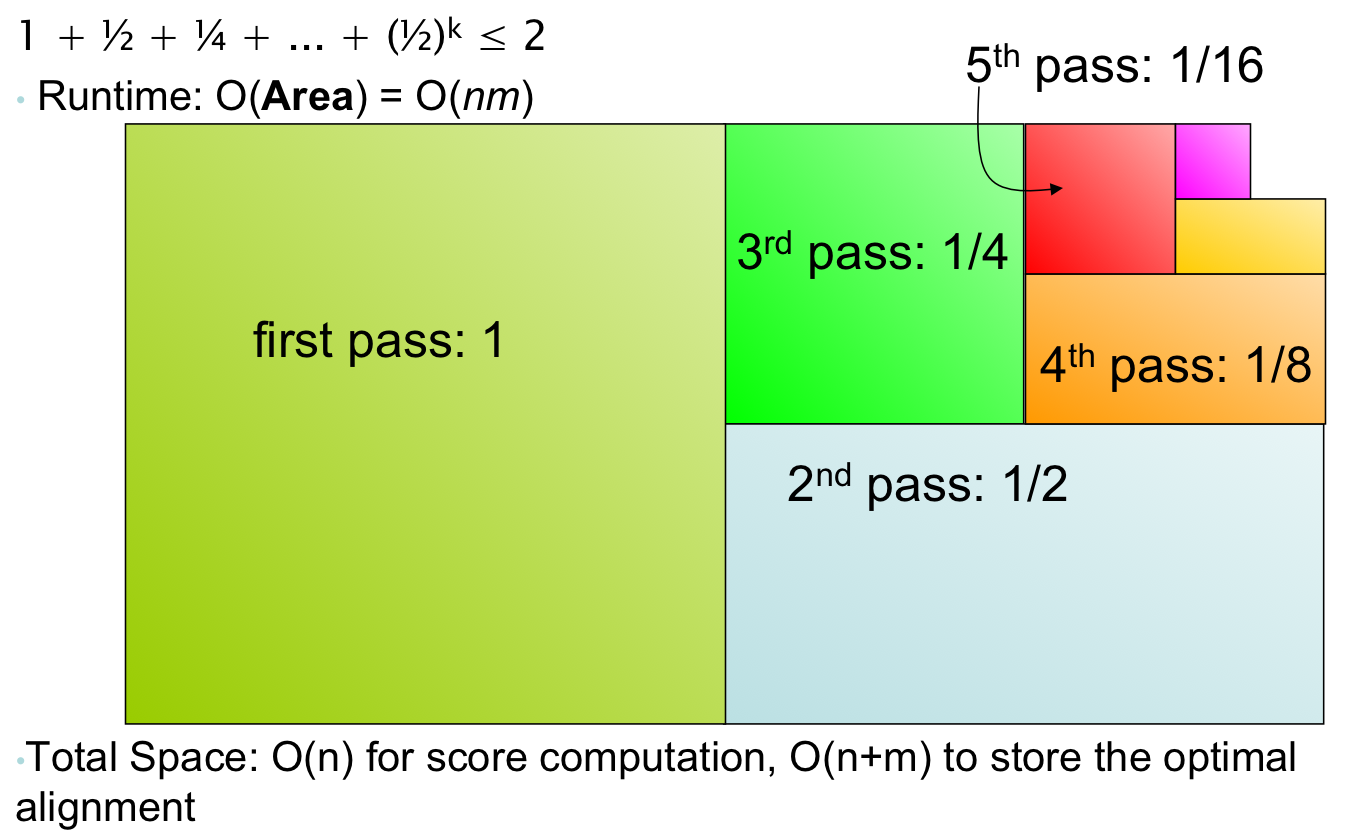
Algorithm's Performance

  • On first level, the algorithm fills every entry in the matrix, thus it does $O(nm)$ work

17

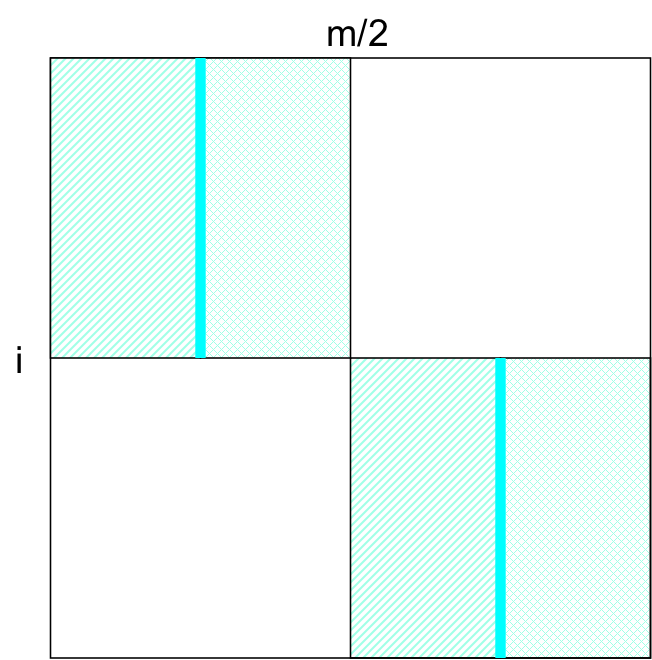
Work done on a second pass

  • On second level, the algorithm fills half the entries in the matrix, thus it does $O(nm)/2$ work

18

Work done on an Alternate second pass

  • This is true regardless of what mid is

19

Work done on a third pass

  • On the third level, the algorithm fills a quarter of the entries in the matrix, thus it does $O(nm)/4$ work

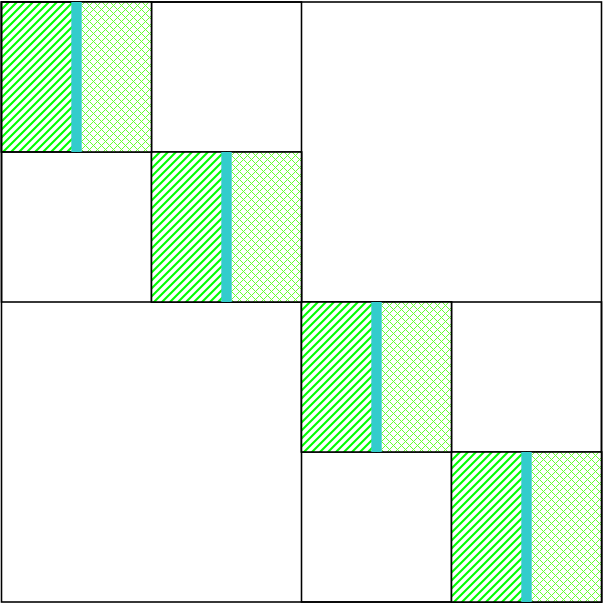
20

Sum of a Geometric Series

21

Can We Do Even Better?

  • Align in Subquadratic Time?
  • Dynamic Programming takes O(nm) for global alignment, which is quadratic assuming n ≈ m
  • Yes, using the Four-Russians Speedup

22

Partitioning the Alignment Grid

Into smaller blocks

23

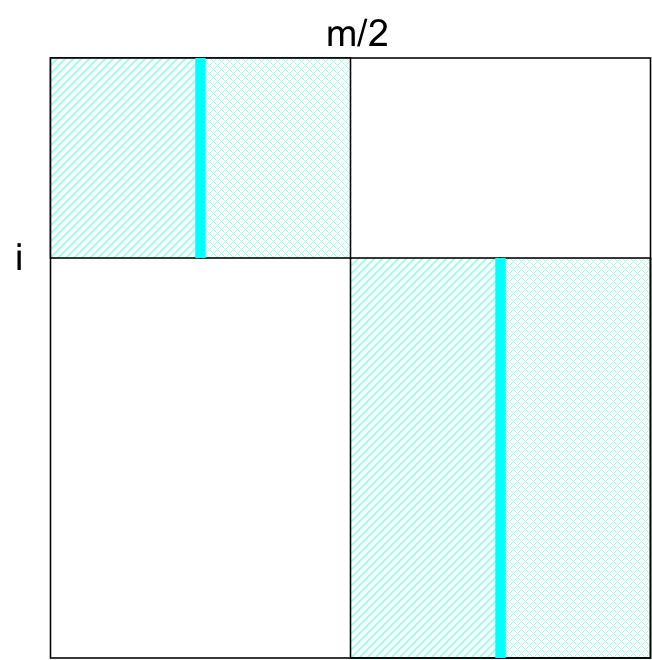
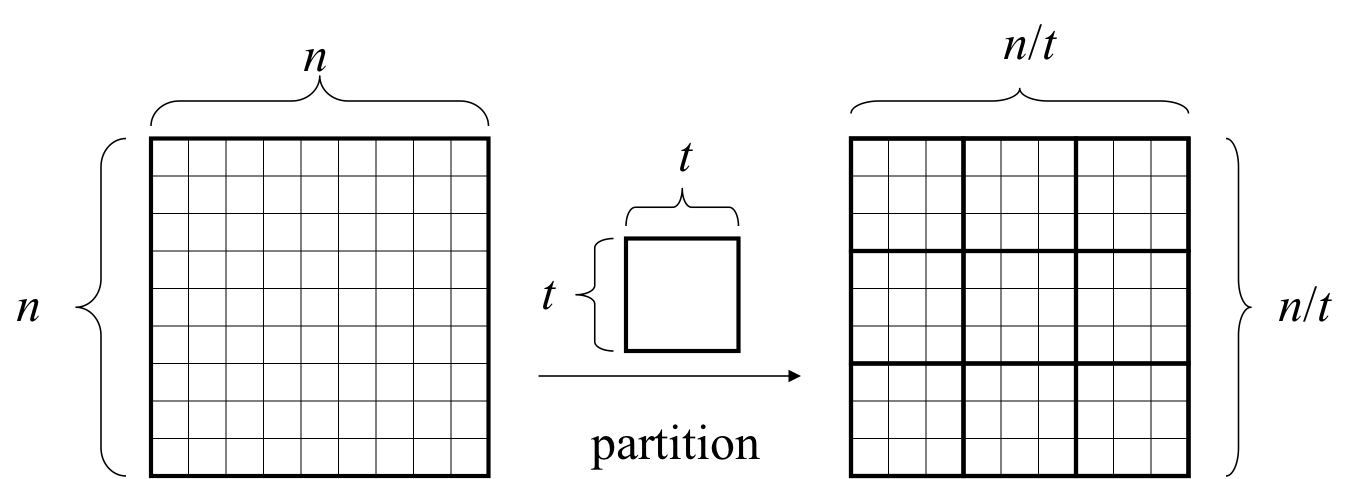
Block Logic

  • How does a block relate to a correct alignment?

    • the alignment path passes through block
    • the path does not use the block

  • The alignment passes through O(n/t) total blocks

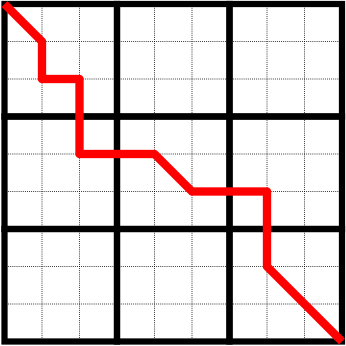
  • Paths enter from the top or left and exit from the right or bottom

  • If we know the best score at the boundaries, perhaps we can peice together a solution as we did before.

24

Recall our Bag of Tricks

  • A key insight of dynamic programming was to reuse repeated computations by storing them in a tableau
  • Are there any repeated computations in Block Alignments?
  • Let’s check out some numbers…
    • Lets assume n = m = 4000 and t = 4
    • n/t = 1000, so there are 1,000,000 blocks
    • How many possible many blocks are there?
      • Assume we are aligning DNA with DNA, so there sequences are over an alphabet of {A,C,G,T}
      • Possible sequences are 4t = 44 = 256,
      • Possible alignments are 4t x 4t = 65536
  • There are fewer possible alignments than blocks, thus we must be frequently revisiting block alignments!

25

In [ ]: