From Last Time¶
What we learned from a related "Minimal Superstring" problem
- Can be constructed by finding a Hamiltonian path of an n-dimensional De Bruijn graph over k symbols
- Brute-force method is explores all $V!$ paths through $V$ vertices
- Branch-and-Bound method considers only paths composed of edges
- Finding a Hamiltonian path is an NP-complete problem
- There is no known method that can solve it efficiently as the number of vertices grows
- Can be constructed by finding a Eulerian path of a (n−1)-dimensional De Bruijn graph.
- Euler's method finds a path using all edges in $O(E) \equiv O(V^2)$ steps
- Graph must statisfy contraints to be sure that a solution exists
- All but two vertices must be balanced
- The other two must be semi-balanced
2
Applications to Assembling Genomes¶
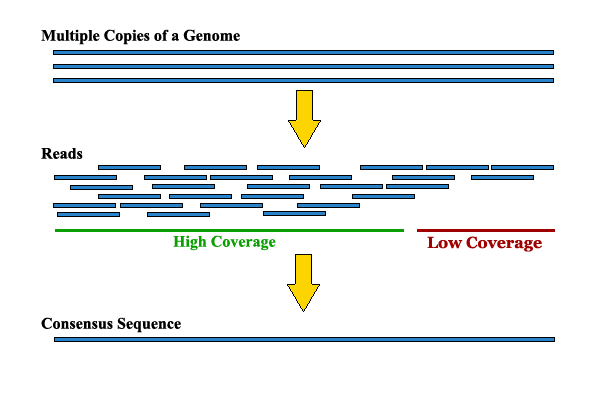
- Extracted DNA is broken into random small fragments
- 100-200 bases are read from one or both ends of the fragment
- Typically, each base of the genome is covered by 10x - 30x fragments
3
Genome Assembly vs Minimal Superstring¶
- Mininmal substring problem
- Every k-mer are known and used as a vertex, (all $\sigma^k$)
- Paths, and there may be multiple, are solutions
- Read fragments
- No guarentee that we will see every k-mer
- Can't disambiguate repeats
4
A Small Example¶
GACGGCGGCGCACGGCGCAA - Our toy sequence from 2 lectures ago
GACGG CGCAC
ACGGC GCACG
CGGCG CACGG - The complete set of 16 5-mers
GGCGG ACGGC
GCGGC CGGCG
CGGCG GGCGC
GGCGC GCGCA
GGCGA CGCAA
- All k-mers is equivalent to kx coverage
- Four repeated k-mers {ACGGC, CGGCG, GCGCA, GGCGC}
5
Some Code¶
- First let's add a function to uniquely label repeated k-mers
In [25]:
def kmersUnique(seq, k):
kmers = sorted([seq[i:i+k] for i in xrange(len(seq)-k+1)])
for i in xrange(1,len(kmers)):
if (kmers[i] == kmers[i-1][0:k]):
t = kmers[i-1].find('_')
if (t >= 0):
n = int(kmers[i-1][t+1:]) + 1
kmers[i] = kmers[i] + "_" + str(n)
else:
kmers[i-1] = kmers[i-1] + "_1"
kmers[i] = kmers[i] + "_2"
return kmers
kmers = kmersUnique("GACGGCGGCGCACGGCGCAA", 5)
print kmers
- Our Graph Class from last lecture
In [27]:
import itertools
class Graph:
def __init__(self, vlist=[]):
""" Initialize a Graph with an optional vertex list """
self.index = {v:i for i,v in enumerate(vlist)}
self.vertex = {i:v for i,v in enumerate(vlist)}
self.edge = []
self.edgelabel = []
def addVertex(self, label):
""" Add a labeled vertex to the graph """
index = len(self.index)
self.index[label] = index
self.vertex[index] = label
def addEdge(self, vsrc, vdst, label='', repeats=True):
""" Add a directed edge to the graph, with an optional label.
Repeated edges are distinct, unless repeats is set to False. """
e = (self.index[vsrc], self.index[vdst])
if (repeats) or (e not in self.edge):
self.edge.append(e)
self.edgelabel.append(label)
def hamiltonianPath(self):
""" A Brute-force method for finding a Hamiltonian Path.
Basically, all possible N! paths are enumerated and checked
for edges. Since edges can be reused there are no distictions
made for *which* version of a repeated edge. """
for path in itertools.permutations(sorted(self.index.values())):
for i in xrange(len(path)-1):
if ((path[i],path[i+1]) not in self.edge):
break
else:
return [self.vertex[i] for i in path]
return []
def SearchTree(self, path, verticesLeft):
""" A recursive Branch-and-Bound Hamiltonian Path search.
Paths are extended one node at a time using only available
edges from the graph. """
if (len(verticesLeft) == 0):
self.PathV2result = [self.vertex[i] for i in path]
return True
for v in verticesLeft:
if (len(path) == 0) or ((path[-1],v) in self.edge):
if self.SearchTree(path+[v], [r for r in verticesLeft if r != v]):
return True
return False
def hamiltonianPathV2(self):
""" A wrapper function for invoking the Branch-and-Bound
Hamiltonian Path search. """
self.PathV2result = []
self.SearchTree([],sorted(self.index.values()))
return self.PathV2result
def degrees(self):
""" Returns two dictionaries with the inDegree and outDegree
of each node from the graph. """
inDegree = {}
outDegree = {}
for src, dst in self.edge:
outDegree[src] = outDegree.get(src, 0) + 1
inDegree[dst] = inDegree.get(dst, 0) + 1
return inDegree, outDegree
def verifyAndGetStart(self):
inDegree, outDegree = self.degrees()
start = 0
end = 0
for vert in self.vertex.iterkeys():
ins = inDegree.get(vert,0)
outs = outDegree.get(vert,0)
if (ins == outs):
continue
elif (ins - outs == 1):
end = vert
elif (outs - ins == 1):
start = vert
else:
start, end = -1, -1
break
if (start >= 0) and (end >= 0):
return start
else:
return -1
def eulerianPath(self):
graph = [(src,dst) for src,dst in self.edge]
currentVertex = self.verifyAndGetStart()
path = [currentVertex]
# "next" is where vertices get inserted into our tour
# it starts at the end (i.e. it is the same as appending),
# but later "side-trips" will insert in the middle
next = 1
while len(graph) > 0:
for edge in graph:
if (edge[0] == currentVertex):
currentVertex = edge[1]
graph.remove(edge)
path.insert(next, currentVertex)
next += 1
break
else:
for edge in graph:
try:
next = path.index(edge[0]) + 1
currentVertex = edge[0]
break
except ValueError:
continue
else:
print "There is no path!"
return False
return path
def eulerEdges(self, path):
edgeId = {}
for i in xrange(len(self.edge)):
edgeId[self.edge[i]] = edgeId.get(self.edge[i], []) + [i]
edgeList = []
for i in xrange(len(path)-1):
edgeList.append(self.edgelabel[edgeId[path[i],path[i+1]].pop()])
return edgeList
def render(self, highlightPath=[]):
""" Outputs a version of the graph that can be rendered
using graphviz tools (http://www.graphviz.org/)."""
edgeId = {}
for i in xrange(len(self.edge)):
edgeId[self.edge[i]] = edgeId.get(self.edge[i], []) + [i]
edgeSet = set()
for i in xrange(len(highlightPath)-1):
src = self.index[highlightPath[i]]
dst = self.index[highlightPath[i+1]]
edgeSet.add(edgeId[src,dst].pop())
result = ''
result += 'digraph {\n'
result += ' graph [nodesep=2, size="10,10"];\n'
for index, label in self.vertex.iteritems():
result += ' N%d [shape="box", style="rounded", label="%s"];\n' % (index, label)
for i, e in enumerate(self.edge):
src, dst = e
result += ' N%d -> N%d' % (src, dst)
label = self.edgelabel[i]
if (len(label) > 0):
if (i in edgeSet):
result += ' [label="%s", penwidth=3.0]' % (label)
else:
result += ' [label="%s"]' % (label)
elif (i in edgeSet):
result += ' [penwidth=3.0]'
result += ';\n'
result += ' overlap=false;\n'
result += '}\n'
return result
6
Finding Paths in our K-mer De Bruijn Graphs¶
In [28]:
k = 5
target = "GACGGCGGCGCACGGCGCAA"
kmers = kmersUnique(target, k)
G1 = Graph(kmers)
for vsrc in kmers:
for vdst in kmers:
if (vsrc[1:k] == vdst[0:k-1]):
G1.addEdge(vsrc,vdst)
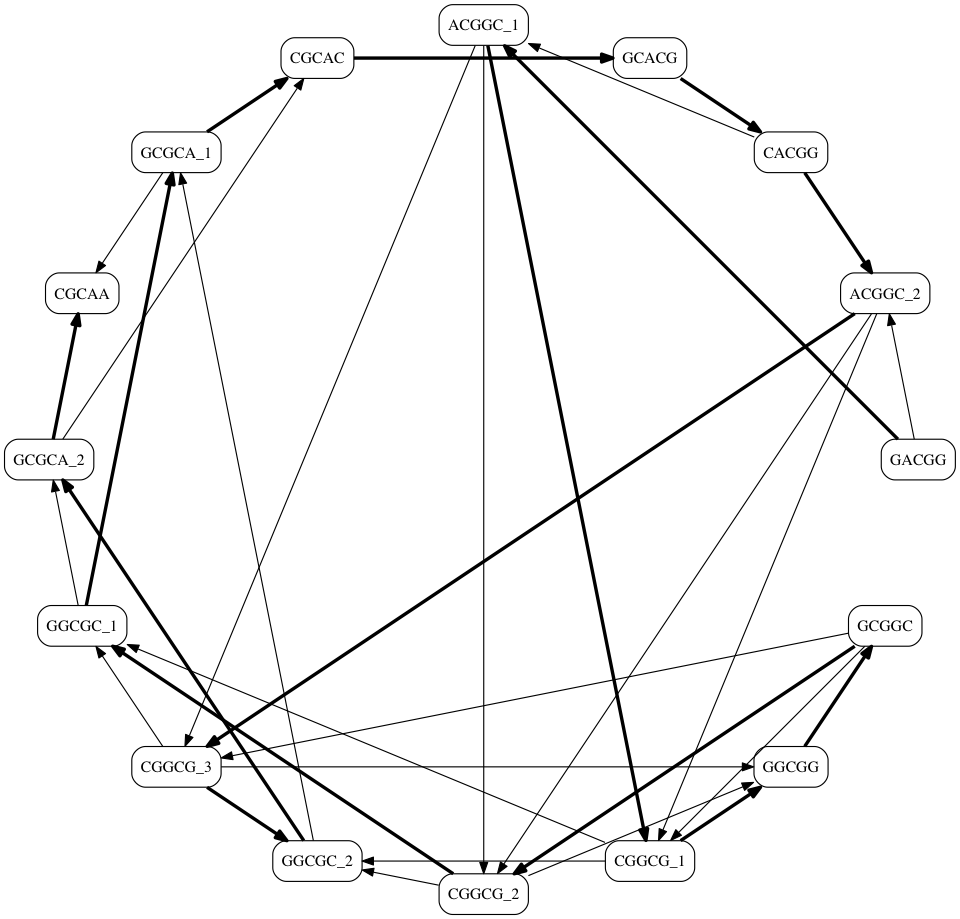
path = G1.hamiltonianPathV2()
print path
seq = path[0][0:k]
for kmer in path[1:]:
seq += kmer[k-1]
print seq
print seq == target
7
What's the Problem?¶
- There are many possible Hamiltonian Paths
How do they differ?
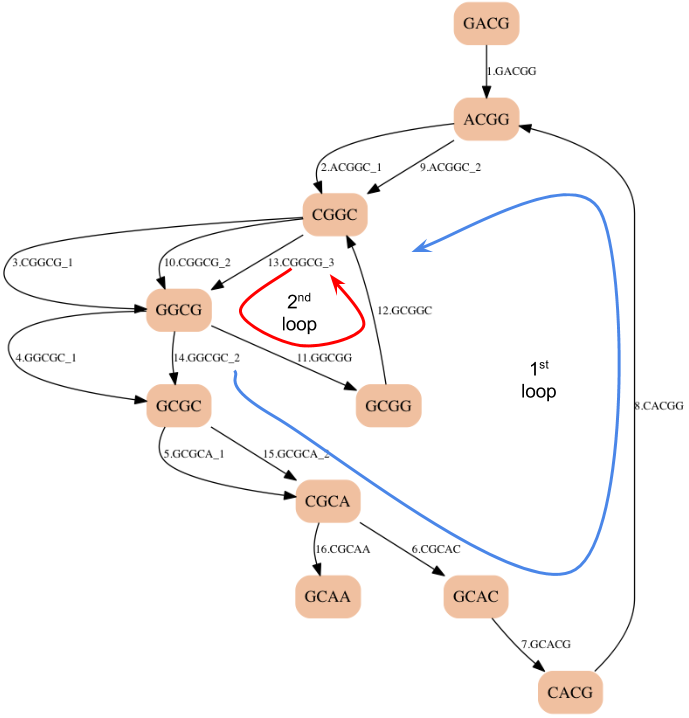
- There were two possible paths leaving any [CGGCG] node
- [CGGCG] → [GGCGC]
- [CGGCG] → [GGCGG]
- A valid solution can be found down either path
- There were two possible paths leaving any [CGGCG] node
There might be even more solutions
Genome assembly is not as unambiguous as the Minimal Substring problem
9
How about an Euler Path?¶
In [29]:
k = 5
target = "GACGGCGGCGCACGGCGCAA"
kmers = kmersUnique(target, k)
print kmers
nodes = sorted(set([code[:k-1] for code in kmers] + [code[1:k] for code in kmers]))
print nodes
G2 = Graph(nodes)
for code in kmers:
G2.addEdge(code[:k-1],code[1:k],code)
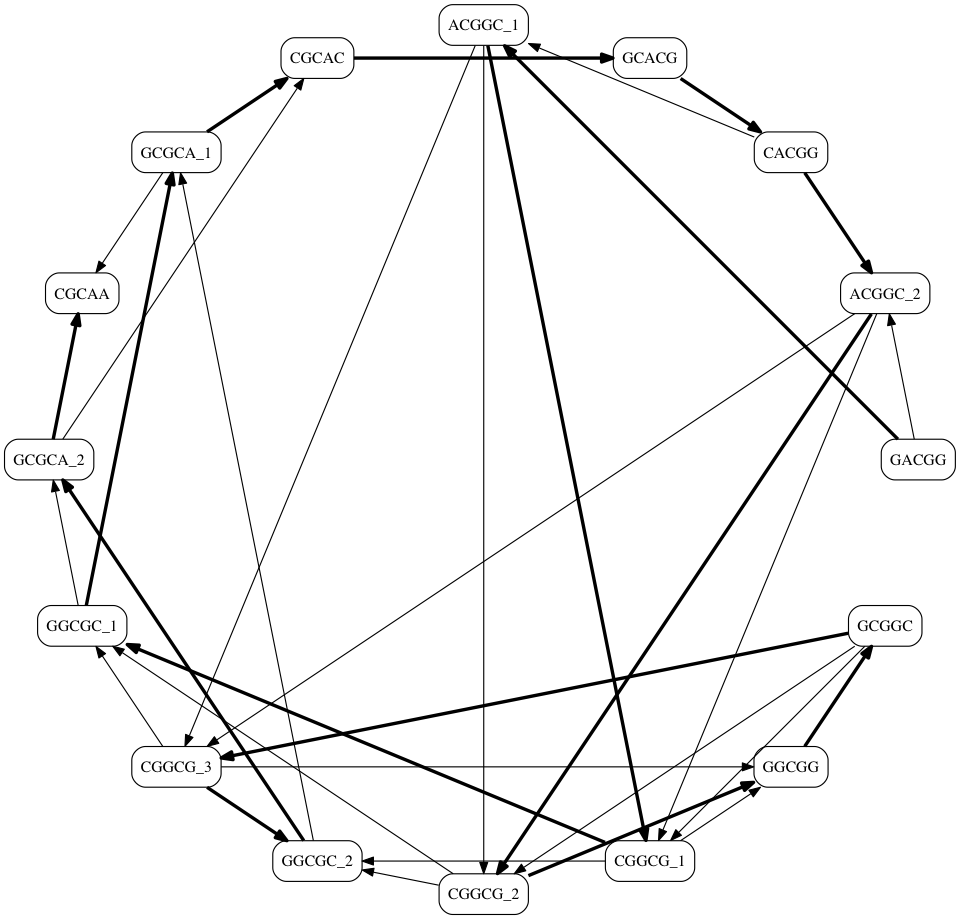
path = G2.eulerianPath()
print path
path = G2.eulerEdges(path)
print path
seq = path[0][0:k]
for kmer in path[1:]:
seq += kmer[k-1]
print seq
print seq == target
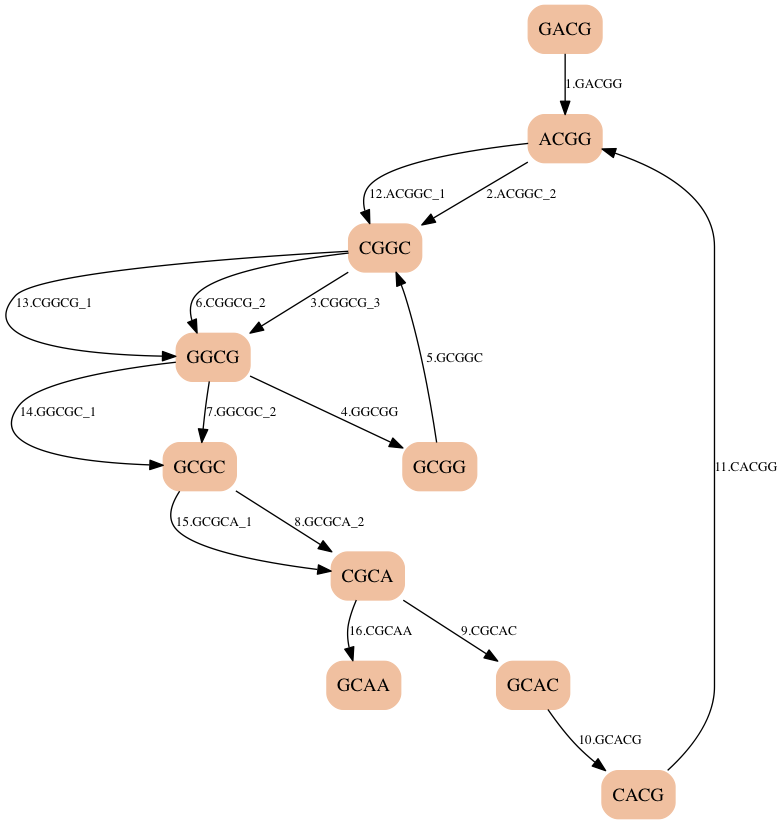
- We got the right answer, but we were lucky.
- There is a path in this graph that matches the Hamiltonian path that we found before
10
A bigger k-mer¶
In [30]:
k = 8
target = "GACGGCGGCGCACGGCGCAA"
kmers = kmersUnique(target, k)
print kmers
nodes = sorted(set([code[:k-1] for code in kmers] + [code[1:k] for code in kmers]))
print nodes
G3 = Graph(nodes)
for code in kmers:
G3.addEdge(code[:k-1],code[1:k],code)
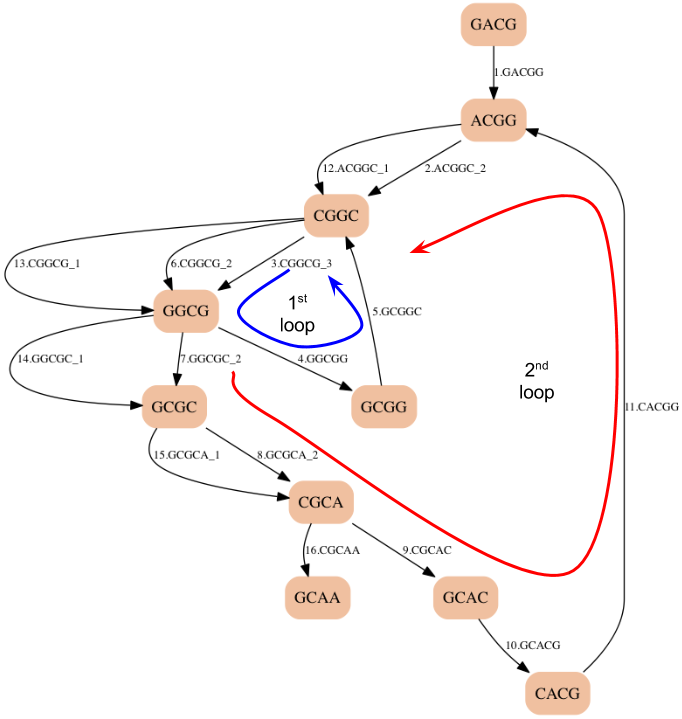
path = G3.eulerianPath()
print path
path = G3.eulerEdges(path)
print path
seq = path[0][0:k]
for kmer in path[1:]:
seq += kmer[k-1]
print seq
print seq == target
- Making k larger (8) eliminates the second choice of loops
- There are edges to choose from, but they all lead to the same path of vertices
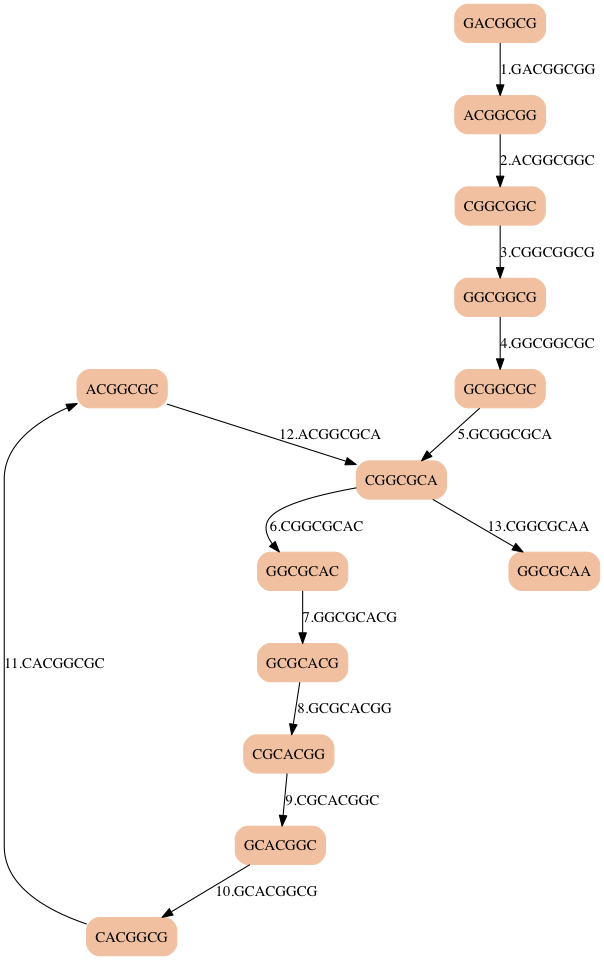
12
Applied to the Hamiltonian Solution¶
In [16]:
k = 8
target = "GACGGCGGCGCACGGCGCAA"
kmers = kmersUnique(target, k)
G4 = Graph(kmers)
for vsrc in kmers:
for vdst in kmers:
if (vsrc[1:k] == vdst[0:k-1]):
G4.addEdge(vsrc,vdst)
path = G4.hamiltonianPathV2()
print path
seq = path[0][0:k]
for kmer in path[1:]:
seq += kmer[k-1]
print seq
print seq == target
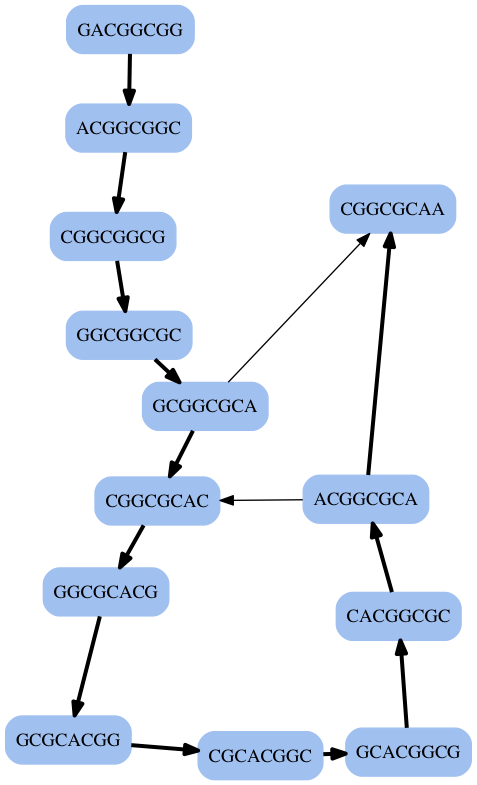
13
Assembly in Reality¶
- Problems with repeated k-mers
- We can't tell a truly repeated k-mer from a copy
- Recall we knew from our example that were {2:ACGGC, 3:CGGCG, 2:GCGCA, 2:GGCGC}
- Assembling path without repeats:
- We can't tell a truly repeated k-mer from a copy
In [24]:
k = 5
target = "GACGGCGGCGCACGGCGCAA"
kmers = set([target[i:i+k] for i in xrange(len(target)-k+1)])
nodes = sorted(set([code[:k-1] for code in kmers] + [code[1:k] for code in kmers]))
G5 = Graph(nodes)
for code in kmers:
G5.addEdge(code[:k-1],code[1:k],code)
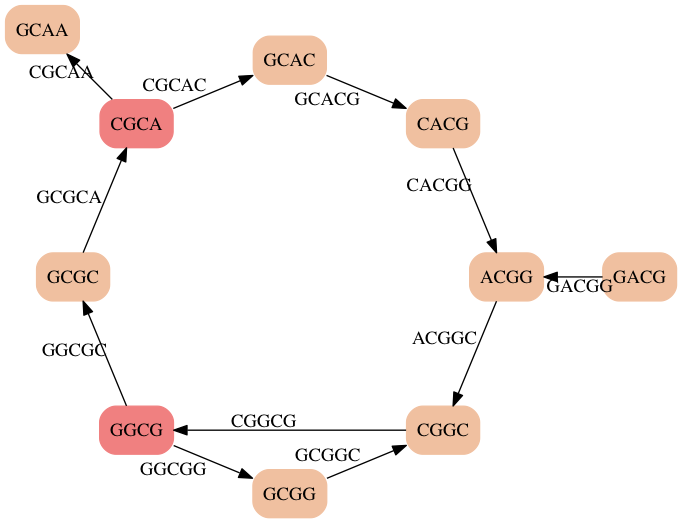
- There is no single Euler Path
- But there are is a set of paths that covers all edges ['GACGGCG', 'GGCGGC', 'GGCGCA', 'CGCAA', 'CGCACGG' ]
- Extend a sequence from a node until you reach a node with an out-degree > 1
- Save these sequences, call them contigs
- Start new contigs following each out-going edge at the branching nodes
- Use a modified read-overlap graph to assemble these contigs
- Add edge-weights that indicate the amount of overlap
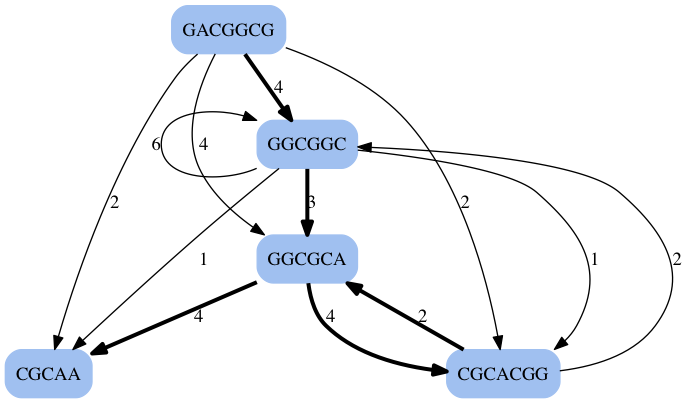
- Usually much smaller than the graph made from k-mers
14