From Last Time¶
Two methods for assembling the 5-mers from the sequence "GACGGCGGCGCACGGCGCAA"
|
||
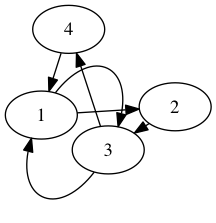
Hamiltonian Path: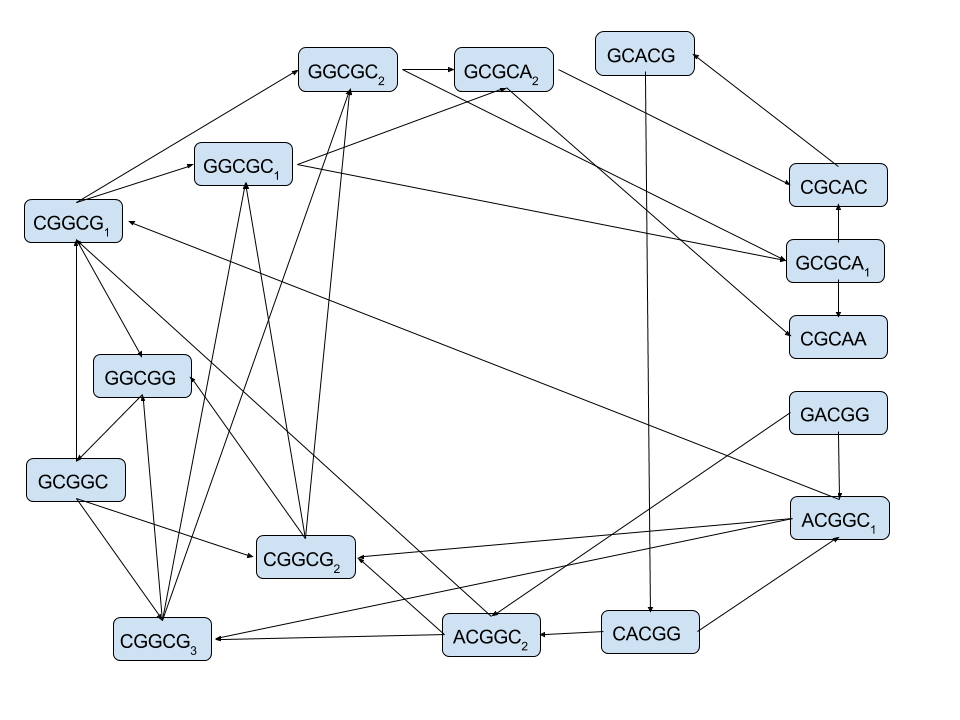
Find a path that passes through every vertex of this graph exactly once.
|
Eulerian Path: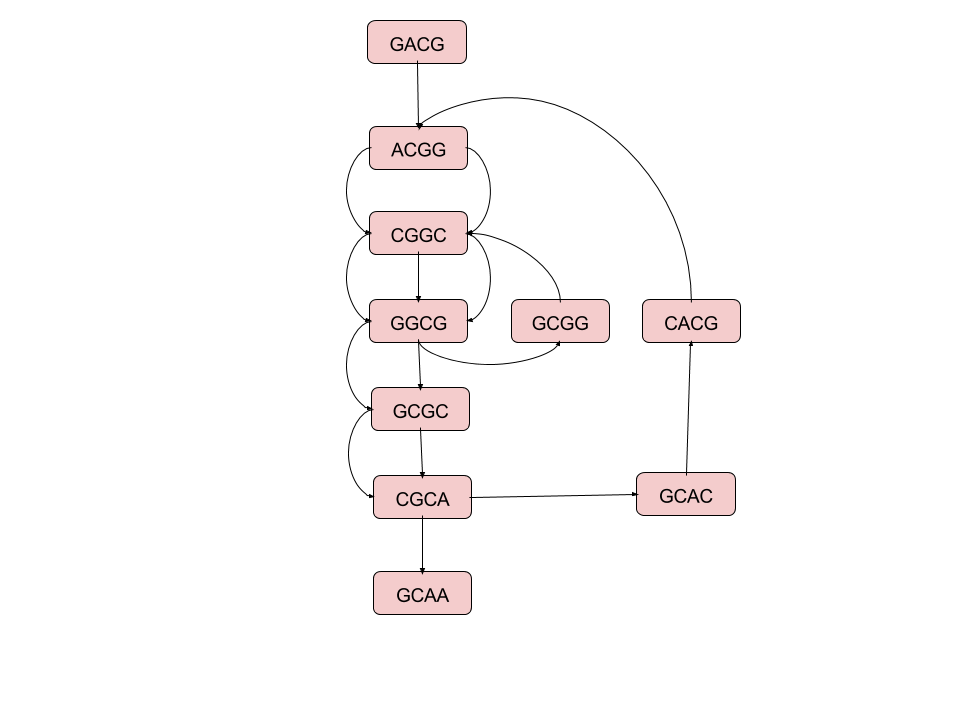
Find a path that passes through every edge of this graph exactly once.
|
|
2
De Bruijn's Problem¶
Nicolaas de Bruijn (1918-2012)
A dutch mathematician noted for his many contributions in the fields of graph theory, number theory, combinatorics and logic.
|
Minimal Superstring Problem:Find the shortest sequence that contains all $\left|\Sigma\right|^k$ strings of length $k$ from the alphabet $\Sigma$ as a substring.
Example: All strings of length 3 from the alphabet {'0','1'}. 
He solved this problem by mapping it to a graph. Note, this particular problem leads to cyclic sequence. |
3
De Bruijn's Graphs¶
|
Minimal Superstrings can be constructed by taking a Hamiltonian path of an n-dimensional De Bruijn graph over k symbols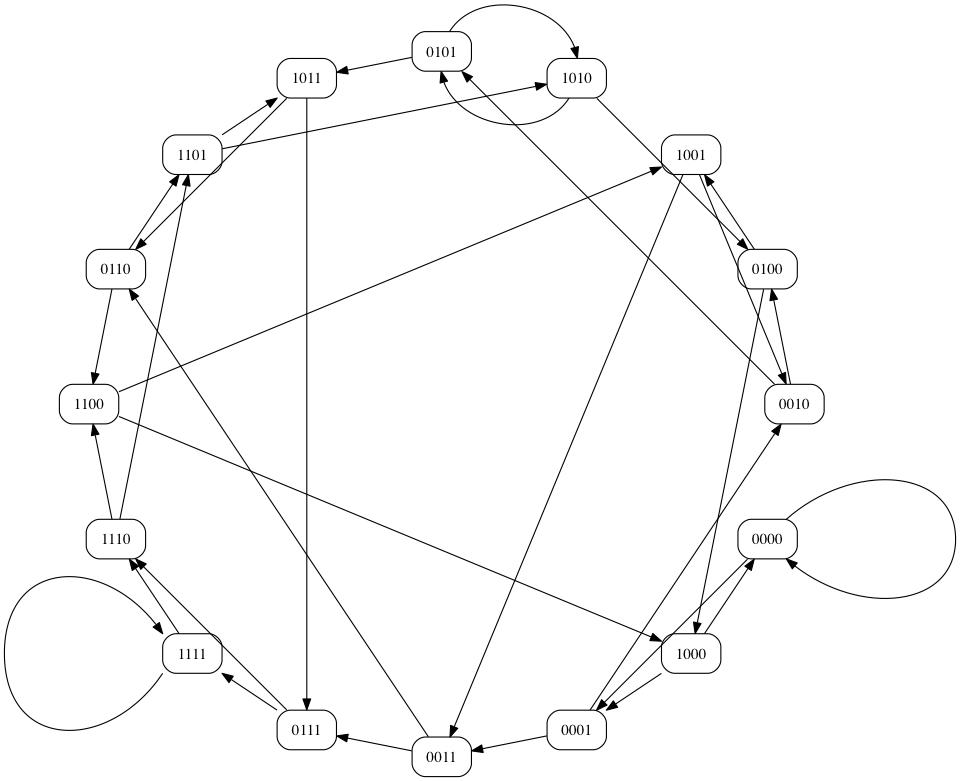 
|
Or, equivalently, a Eulerian cycle of a 
|
4
Solving Graph Problems on a Computer¶
- Graph Representations
|
An example graph: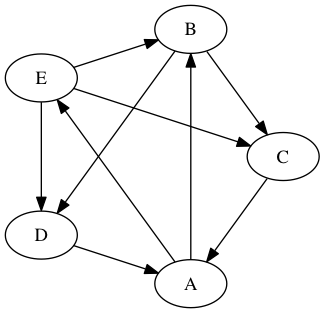 
|
An Adjacency Matrix:
An n × n matrix where Aij is 1 if there is an edge connecting the ith vertex to the jth vertex and 0 otherwise. |
Adjacency Lists: Edge = [(0,1), (0,4), An array or list of vertex pairs (i,j) indicating an edge from the ith vertex to the jth vertex. |
5
Let's write some code¶
In [16]:
class Graph:
def __init__(self, vlist=[]):
""" Initialize a Graph with an optional vertex list """
self.index = {v:i for i,v in enumerate(vlist)}
self.vertex = {i:v for i,v in enumerate(vlist)}
self.edge = []
self.edgelabel = []
def addVertex(self, label):
""" Add a labeled vertex to the graph """
index = len(self.index)
self.index[label] = index
self.vertex[index] = label
def addEdge(self, vsrc, vdst, label='', repeats=True):
""" Add a directed edge to the graph, with an optional label.
Repeated edges are distinct, unless repeats is set to False. """
e = (self.index[vsrc], self.index[vdst])
if (repeats) or (e not in self.edge):
self.edge.append(e)
self.edgelabel.append(label)
Now let's generate the vertices needed to find De Bruijn's superstring of 4-bit binary strings...
In [17]:
import itertools
binary = [''.join(t) for t in itertools.product('01', repeat=4)]
print binary
and create a graph object using them.
In [18]:
G1 = Graph(binary)
for vsrc in binary:
G1.addEdge(vsrc,vsrc[1:]+'0')
G1.addEdge(vsrc,vsrc[1:]+'1')
print
print "Vertex indices = ", G1.index
print
print "Index to Vertex = ",G1.vertex
print
print "Edges = ", G1.edge
The resulting graph:
6
The Hamiltonian Path Problem¶
Next, we need an algorithm to find a path in a graph that visits every node exactly once, if such a path exists.
How?¶
Approach:¶
- Enumerate every possible path (all permutations of N vertices). Python's
itertools.permutations()does this. - Verify that there is an edge connecting all N-1 pairs of adjacent vertices
7
In [19]:
import itertools
for path in itertools.permutations([0,1,2,3]):
print path
Only some of these vertex permutions are actual paths in the graph
8
A Hamiltonian Path Algorithm¶
- Test each vertex permutation to see if it is a valid path
our new Graph class
In [20]:
import itertools
class Graph:
def __init__(self, vlist=[]):
""" Initialize a Graph with an optional vertex list """
self.index = {v:i for i,v in enumerate(vlist)}
self.vertex = {i:v for i,v in enumerate(vlist)}
self.edge = []
self.edgelabel = []
def addVertex(self, label):
""" Add a labeled vertex to the graph """
index = len(self.index)
self.index[label] = index
self.vertex[index] = label
def addEdge(self, vsrc, vdst, label='', repeats=True):
""" Add a directed edge to the graph, with an optional label.
Repeated edges are distinct, unless repeats is set to False. """
e = (self.index[vsrc], self.index[vdst])
if (repeats) or (e not in self.edge):
self.edge.append(e)
self.edgelabel.append(label)
def hamiltonianPath(self):
""" A Brute-force method for finding a Hamiltonian Path.
Basically, all possible N! paths are enumerated and checked
for edges. Since edges can be reused there are no distictions
made for *which* version of a repeated edge. """
for path in itertools.permutations(sorted(self.index.values())):
for i in xrange(len(path)-1):
if ((path[i],path[i+1]) not in self.edge):
break
else:
return [self.vertex[i] for i in path]
return []
Create the superstring graph and find a Hamiltonian Path
In [21]:
G1 = Graph(binary)
for vsrc in binary:
G1.addEdge(vsrc,vsrc[1:]+'0')
G1.addEdge(vsrc,vsrc[1:]+'1')
# WARNING: takes about 30 mins
%time path = G1.hamiltonianPath()
print path
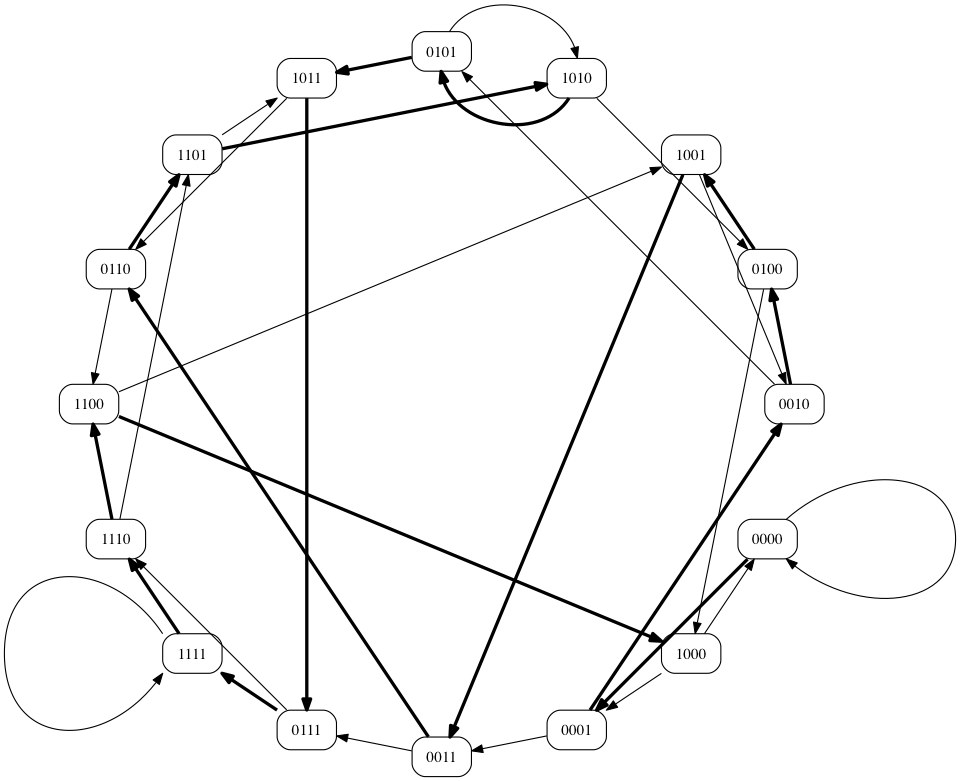
9
Is our Solution Unique?¶
How about the path = ["0000", "0001", "0011", "0111", "1111", "1110", "1101", "1010", "0100", "1001", "0010", "0101", "1011", "0110", "1100", "1000"]
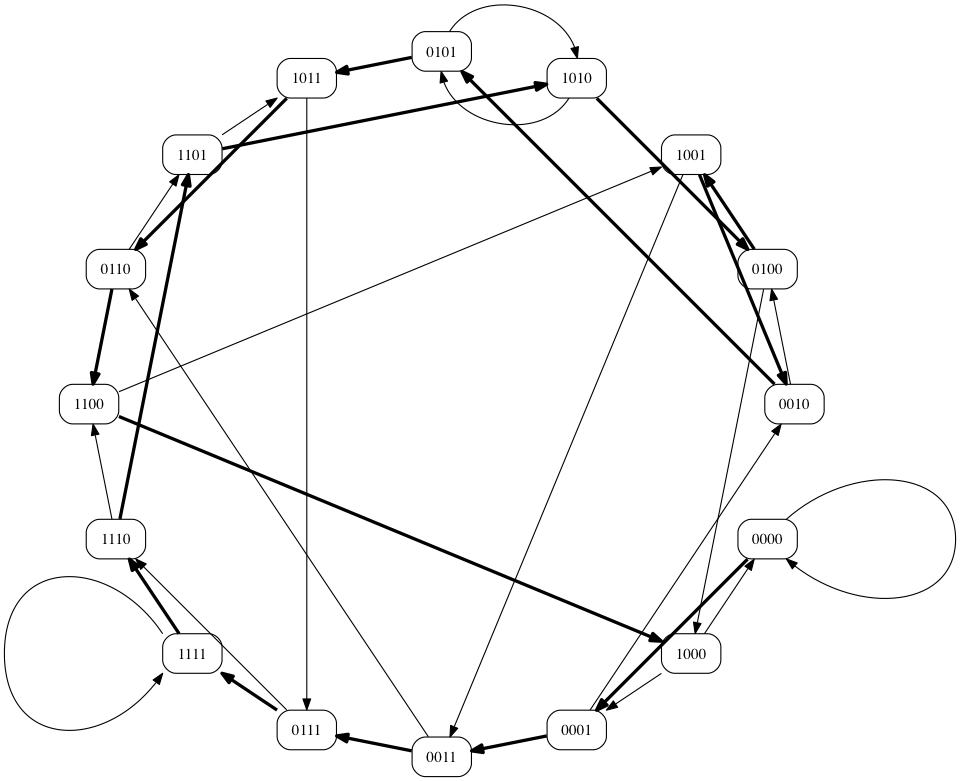
- Our Hamiltonian Path finder produces a single path if one exists.
- How would you modify it to produce every valid Hamiltonian path?
- How long would that take?
One of De Bruijn's contributions is that there are:
$$\frac{(\sigma!)^{\sigma^{k-1}}}{\sigma^k}$$paths leading to superstrings where $\sigma = \left|\Sigma\right|$.
In our case $\sigma = 2$ and k = 4, so there should be $\frac{2^{2^3}}{2^4} = 16$ paths (ignoring those that are just different starting points on the same cycle)
10
Brute Force is Slow¶
- There are N! possible paths for N vertices.
- Our 16 vertices give 20,922,789,888,000 possible paths
- There is a fairly simple Branch-and-Bound evaluation strategy
- Grow the path using only valid edges
11
A Branch-and-Bound Hamiltonian Path Finder¶
- Use recursion to extend paths along edges that include any unvisited vertex
- If we use all vertices, we've found a path
- We keep two lists
- The path so far, where each pair of adjacent vertices is connected by an edge
- Unused vertices. When empty we've found a path
In [14]:
import itertools
class Graph:
def __init__(self, vlist=[]):
""" Initialize a Graph with an optional vertex list """
self.index = {v:i for i,v in enumerate(vlist)}
self.vertex = {i:v for i,v in enumerate(vlist)}
self.edge = []
self.edgelabel = []
def addVertex(self, label):
""" Add a labeled vertex to the graph """
index = len(self.index)
self.index[label] = index
self.vertex[index] = label
def addEdge(self, vsrc, vdst, label='', repeats=True):
""" Add a directed edge to the graph, with an optional label.
Repeated edges are distinct, unless repeats is set to False. """
e = (self.index[vsrc], self.index[vdst])
if (repeats) or (e not in self.edge):
self.edge.append(e)
self.edgelabel.append(label)
def hamiltonianPath(self):
""" A Brute-force method for finding a Hamiltonian Path.
Basically, all possible N! paths are enumerated and checked
for edges. Since edges can be reused there are no distictions
made for *which* version of a repeated edge. """
for path in itertools.permutations(sorted(self.index.values())):
for i in xrange(len(path)-1):
if ((path[i],path[i+1]) not in self.edge):
break
else:
return [self.vertex[i] for i in path]
return []
def SearchTree(self, path, verticesLeft):
""" A recursive Branch-and-Bound Hamiltonian Path search.
Paths are extended one node at a time using only available
edges from the graph. """
if (len(verticesLeft) == 0):
self.PathV2result = [self.vertex[i] for i in path]
return True
for v in verticesLeft:
if (len(path) == 0) or ((path[-1],v) in self.edge):
if self.SearchTree(path+[v], [r for r in verticesLeft if r != v]):
return True
return False
def hamiltonianPathV2(self):
""" A wrapper function for invoking the Branch-and-Bound
Hamiltonian Path search. """
self.PathV2result = []
self.SearchTree([],sorted(self.index.values()))
return self.PathV2result
Let's test it with the same graph from before.
In [18]:
G1 = Graph(binary)
for vsrc in binary:
G1.addEdge(vsrc,vsrc[1:]+'0')
G1.addEdge(vsrc,vsrc[1:]+'1')
%time path = G1.hamiltonianPathV2()
print path
superstring = path[0] + ''.join([path[i][3] for i in xrange(1,len(path))])
print superstring
That's a considerable speed up, but it might be slow for some graphs ...
12
Is there a better Hamiltonian Path Algorithm?¶
- Better in what sense
- It requires a number of steps that are polynomial in either the number of edges or vertices
- Polynomial: ${variable}^{constant}$
- Exponential: ${constant}^{variable}$ or worse, ${variable}^{variable}$
- For example our Brute-Force algorithm was $O(V!) = O(V^V)$ where V is the number of vertices in our graph, a problem variable
- All known algorithms are exponential, and exponentials grow so fast that we can only practically solve small problems if the algorithm for solving them take a number of step that grows exponentially with a problem variable (i.e. the number of vertices)
- Can we prove that there is no algorithm that can find a Hamiltonian Path in a time that is polynomial in the number of vertices or edges in the graph?
- No one has
- There is a million-dollar reward to be found if you can!
- A lot of known Hard problems suddenly become solvable using your algorithm
- It requires a number of steps that are polynomial in either the number of edges or vertices
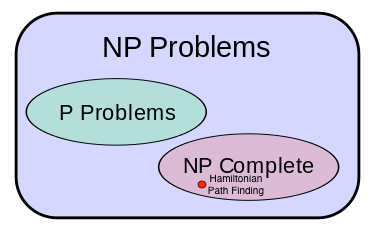
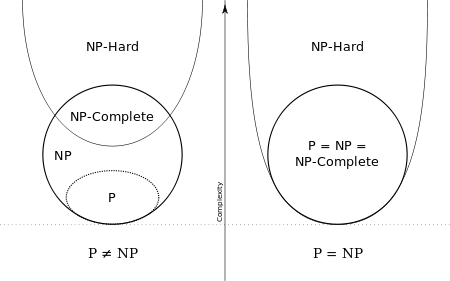
13
De Bruijn's Key Insight¶
|
De Bruijn also realized that Minimal Superstrings were ***Eulerian cycles*** in (k−1)-dimensional "De Bruijn graph" (i.e. a graph where the desired strings are *edges*, and vertices are the (k-1)-mer suffixes and prefixes of the string set). He also knew that Euler had an ingenous way to solve this problem. Recall Euler's desire to counstuct a tour where each bridge was crossed only once.
He didn't solve the general Hamiltonian Path problem, but he was able to remap the Minimal Superstring problem to a simpler problem. Note every Minimal Superstring Problem can be fomulated as a Hamiltonian Path in some graph, but the converse is not true. Instead, he found a clever mapping of every Minimal Superstring Problem to a Eulerian Path problem.
Let's demonstrate using the islands and bridges shown to the right |
|
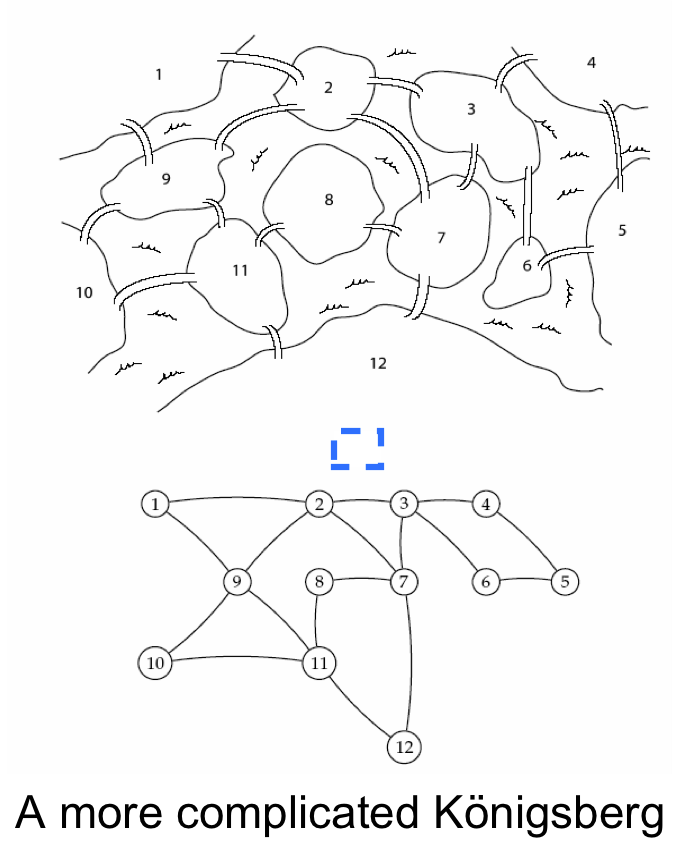
14
Finding an Eulerian Cycle¶
Our first path:
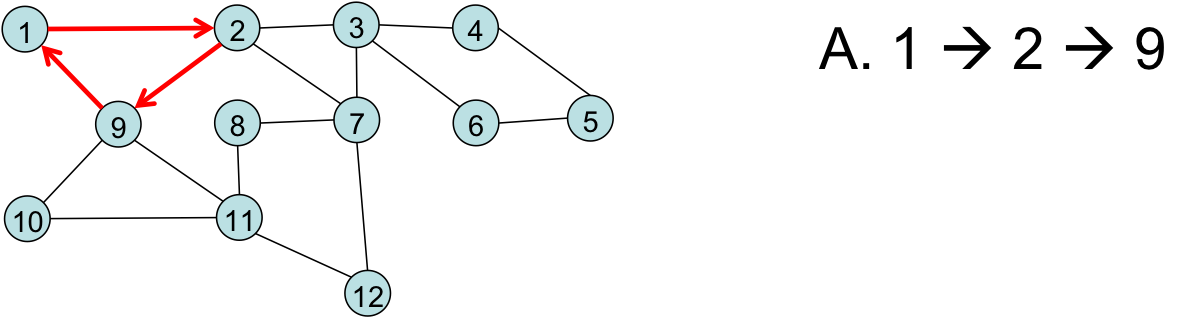
Take a side-trip, and merge it in:
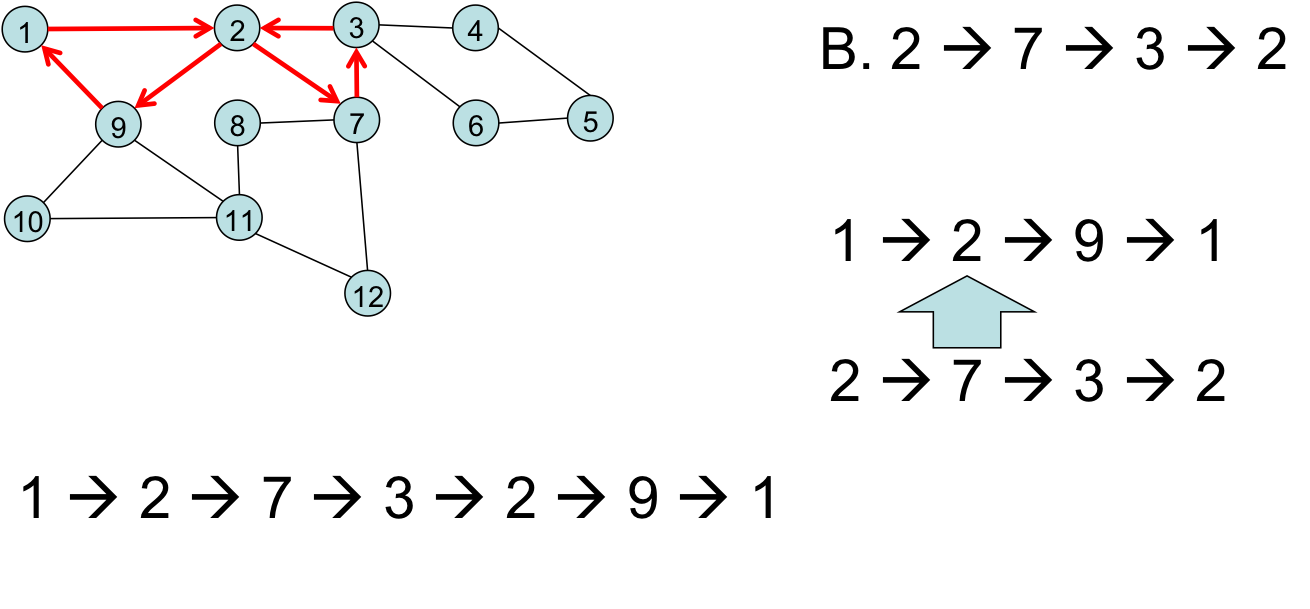
Merging in a second side-trip:
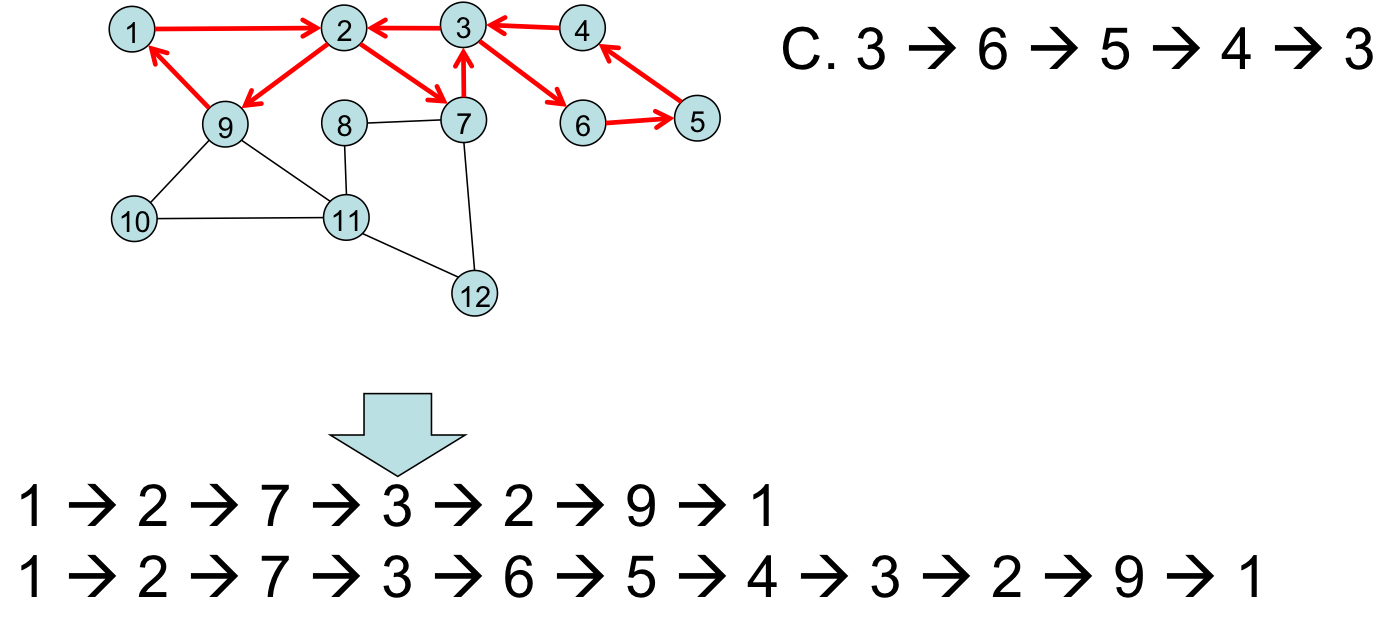
Merging in a third side-trip:
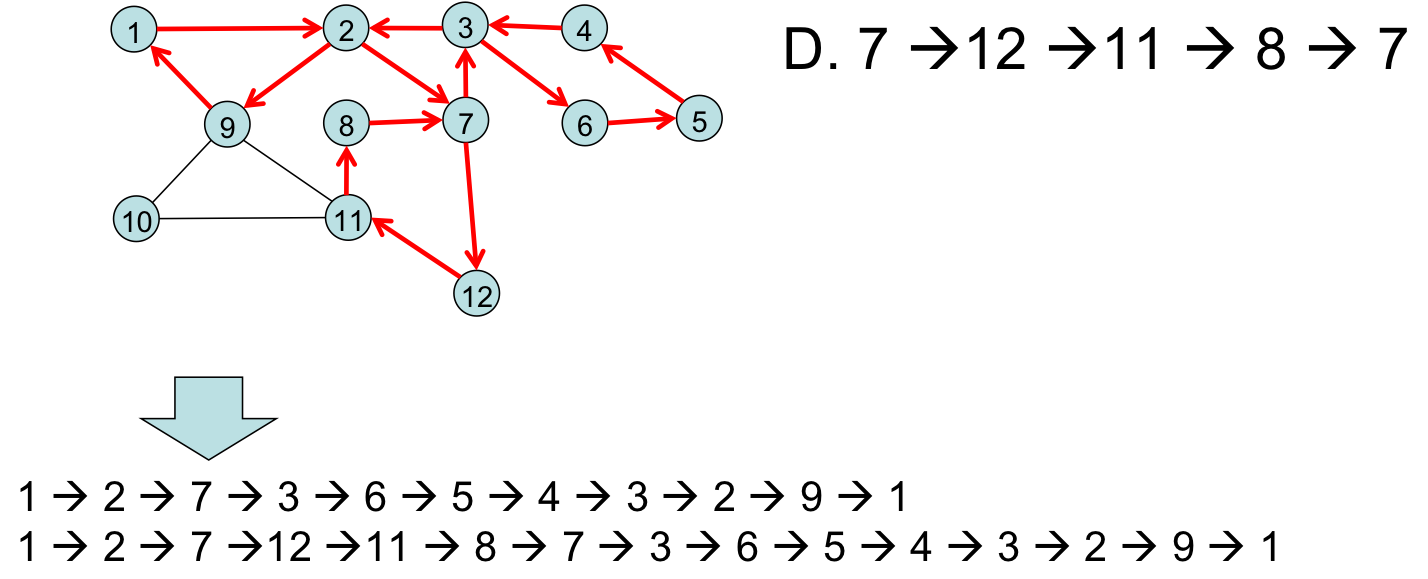
Merging in a final side-trip:
This algorithm requires a number of steps that is linear in the number of graph edges, $O(E)$. The number of edges in a general graph is $E = O(V^2)$ (the adjacency matrix tells us this).
15
Now the code¶
In [6]:
# This is a new method of our Graph Class
def eulerianPath(self):
graph = [(src,dst) for src,dst in self.edge]
currentVertex = self.verifyAndGetStart()
path = [currentVertex]
# "next" is where vertices get inserted into our tour
# it starts at the end (i.e. it is the same as appending),
# but later "side-trips" will insert in the middle
next = 1
while len(graph) > 0:
# follows a path until it ends
for edge in graph:
if (edge[0] == currentVertex):
currentVertex = edge[1]
graph.remove(edge)
path.insert(next, currentVertex)
next += 1
break
else:
# Look for side-trips along the path
for edge in graph:
try:
# insert our side-trip after the
# "u" vertex that is starts from
next = path.index(edge[0]) + 1
currentVertex = edge[0]
break
except ValueError:
continue
else:
print "There is no path!"
return False
return path
Some issues with our code:
- Where do we start our tour? (The mysterious VerifyandGetStart() method)
- Where will it end?
- How do we know that each side-trip will rejoin the graph at the same point where it began?
16
Euler's Theorems¶
- A graph is balanced if for every vertex the number of incoming edges equals to the number of outgoing edges:
- Theorem 1: A connected graph has a Eulerian Cycle if and only if each of its vertices are balanced.
- In mid-tour for every path onto an island there must be another path off
- Exceptions are allowed at the start and end of the tour
- Theorem 2: A connected graph has an Eulerian Path if and only if it contains at exacty two semi-balanced vertices and all others are balanced.
- One of the semi-balanced vertices, with $out(v) = in(v) + 1$ is the start of the tour
- The othersemi-balanced vertex, with $in(v) = out(v) + 1$ is the end of the tour
17
Continuing the Code¶
In [7]:
# More new methods for the Graph Class
def degrees(self):
""" Returns two dictionaries with the inDegree and outDegree
of each node from the graph. """
inDegree = {}
outDegree = {}
for src, dst in self.edge:
outDegree[src] = outDegree.get(src, 0) + 1
inDegree[dst] = inDegree.get(dst, 0) + 1
return inDegree, outDegree
def verifyAndGetStart(self):
inDegree, outDegree = self.degrees()
start = 0
end = 0
for vert in self.vertex.iterkeys():
ins = inDegree.get(vert,0)
outs = outDegree.get(vert,0)
if (ins == outs):
continue
elif (ins - outs == 1):
end = vert
elif (outs - ins == 1):
start = vert
else:
start, end = -1, -1
break
if (start >= 0) and (end >= 0):
return start
else:
return -1
18
A Complete Graph Class¶
In [9]:
import itertools
class Graph:
def __init__(self, vlist=[]):
""" Initialize a Graph with an optional vertex list """
self.index = {v:i for i,v in enumerate(vlist)}
self.vertex = {i:v for i,v in enumerate(vlist)}
self.edge = []
self.edgelabel = []
def addVertex(self, label):
""" Add a labeled vertex to the graph """
index = len(self.index)
self.index[label] = index
self.vertex[index] = label
def addEdge(self, vsrc, vdst, label='', repeats=True):
""" Add a directed edge to the graph, with an optional label.
Repeated edges are distinct, unless repeats is set to False. """
e = (self.index[vsrc], self.index[vdst])
if (repeats) or (e not in self.edge):
self.edge.append(e)
self.edgelabel.append(label)
def hamiltonianPath(self):
""" A Brute-force method for finding a Hamiltonian Path.
Basically, all possible N! paths are enumerated and checked
for edges. Since edges can be reused there are no distictions
made for *which* version of a repeated edge. """
for path in itertools.permutations(sorted(self.index.values())):
for i in xrange(len(path)-1):
if ((path[i],path[i+1]) not in self.edge):
break
else:
return [self.vertex[i] for i in path]
return []
def SearchTree(self, path, verticesLeft):
""" A recursive Branch-and-Bound Hamiltonian Path search.
Paths are extended one node at a time using only available
edges from the graph. """
if (len(verticesLeft) == 0):
self.PathV2result = [self.vertex[i] for i in path]
return True
for v in verticesLeft:
if (len(path) == 0) or ((path[-1],v) in self.edge):
if self.SearchTree(path+[v], [r for r in verticesLeft if r != v]):
return True
return False
def hamiltonianPathV2(self):
""" A wrapper function for invoking the Branch-and-Bound
Hamiltonian Path search. """
self.PathV2result = []
self.SearchTree([],sorted(self.index.values()))
return self.PathV2result
def degrees(self):
""" Returns two dictionaries with the inDegree and outDegree
of each node from the graph. """
inDegree = {}
outDegree = {}
for src, dst in self.edge:
outDegree[src] = outDegree.get(src, 0) + 1
inDegree[dst] = inDegree.get(dst, 0) + 1
return inDegree, outDegree
def verifyAndGetStart(self):
inDegree, outDegree = self.degrees()
start = 0
end = 0
for vert in self.vertex.iterkeys():
ins = inDegree.get(vert,0)
outs = outDegree.get(vert,0)
if (ins == outs):
continue
elif (ins - outs == 1):
end = vert
elif (outs - ins == 1):
start = vert
else:
start, end = -1, -1
break
if (start >= 0) and (end >= 0):
return start
else:
return -1
def eulerianPath(self):
graph = [(src,dst) for src,dst in self.edge]
currentVertex = self.verifyAndGetStart()
path = [currentVertex]
# "next" is where vertices get inserted into our tour
# it starts at the end (i.e. it is the same as appending),
# but later "side-trips" will insert in the middle
next = 1
while len(graph) > 0:
for edge in graph:
if (edge[0] == currentVertex):
currentVertex = edge[1]
graph.remove(edge)
path.insert(next, currentVertex)
next += 1
break
else:
for edge in graph:
try:
next = path.index(edge[0]) + 1
currentVertex = edge[0]
break
except ValueError:
continue
else:
print "There is no path!"
return False
return path
def eulerEdges(self, path):
edgeId = {}
for i in xrange(len(self.edge)):
edgeId[self.edge[i]] = edgeId.get(self.edge[i], []) + [i]
edgeList = []
for i in xrange(len(path)-1):
edgeList.append(self.edgelabel[edgeId[path[i],path[i+1]].pop()])
return edgeList
def render(self, highlightPath=[]):
""" Outputs a version of the graph that can be rendered
using graphviz tools (http://www.graphviz.org/)."""
edgeId = {}
for i in xrange(len(self.edge)):
edgeId[self.edge[i]] = edgeId.get(self.edge[i], []) + [i]
edgeSet = set()
for i in xrange(len(highlightPath)-1):
src = self.index[highlightPath[i]]
dst = self.index[highlightPath[i+1]]
edgeSet.add(edgeId[src,dst].pop())
result = ''
result += 'digraph {\n'
result += ' graph [nodesep=2, size="10,10"];\n'
for index, label in self.vertex.iteritems():
result += ' N%d [shape="box", style="rounded", label="%s"];\n' % (index, label)
for i, e in enumerate(self.edge):
src, dst = e
result += ' N%d -> N%d' % (src, dst)
label = self.edgelabel[i]
if (len(label) > 0):
if (i in edgeSet):
result += ' [label="%s", penwidth=3.0]' % (label)
else:
result += ' [label="%s"]' % (label)
elif (i in edgeSet):
result += ' [penwidth=3.0]'
result += ';\n'
result += ' overlap=false;\n'
result += '}\n'
return result
Note: I also added an eulerEdges() method to the class. The Eulerian Path algorithm returns a list of vertices along the path, which is consistent with the Hamiltonian Path algorithm. However, in our case, we are less interested in the series of vertices visited than we are the series of edges. Thus, eulerEdges(), returns the edge labels along a path.
19
Finding Minimal Superstrings with an Euler Path¶
In [11]:
binary = [''.join(t) for t in itertools.product('01', repeat=4)]
nodes = sorted(set([code[:-1] for code in binary] + [code[1:] for code in binary]))
G2 = Graph(nodes)
for code in binary:
# Here I give each edge a label
G2.addEdge(code[:-1],code[1:],code)
%time path = G2.eulerianPath()
print nodes
print path
print G2.eulerEdges(path)
- In this case our the graph was fully balanced. So the Euler Path is a cycle.
- Our tour starts arbitarily with the first vertex, '000'
20
In [ ]: